复杂度

复杂度包括时间复杂度和空间复杂度

1. 时间复杂度:描述算法的运行时间，O()表示算法最坏情况下运行时间的上界。

快速排序的时间复杂度:O(nlogn)
暴力枚举的复杂度:O(n^2)

从n到log(n)可以通过二分法，递归等方式实现，注意递归的时间复杂度不一定是log(n)

算法超时与电脑配置有关，也与程序的时间复杂度有关

2. 空间复杂度:对程序的御用内存有一个大致的估计。

空间复杂度:
当随着n的增大，输出内存大小不会变时，空间复杂度就是O(1):

int j = 0;
for (int i = 0; i < n; i++) {
    j++;
}

空间复杂度时O(n)的例子:

int* a = new int(n);
for (int i = 0; i < n; i++) {
    a[i] = i;
}

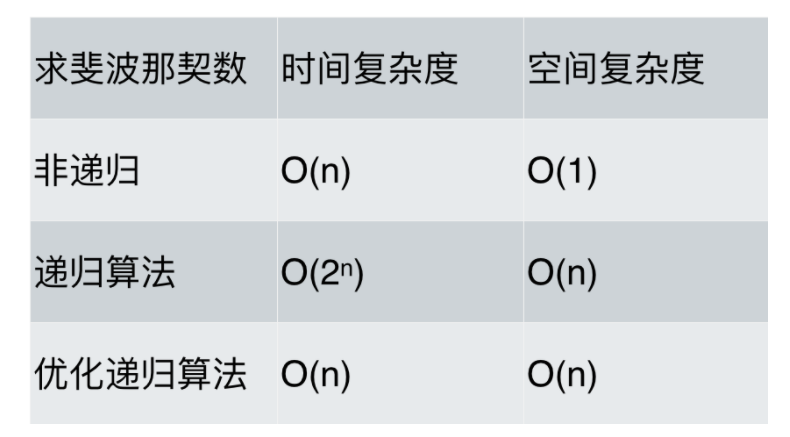
递归的时间复杂度 = 递归的次数 * 每次递归的时间复杂度。

递归的时间复杂度和递归的方式关系很大,下面这种实现fibonacci的方式的时间复杂度是O(2^n).

int fibonacci(int i) {
       if(i <= 0) return 0;
       if(i == 1) return 1;
       return fibonacci(i-1) + fibonacci(i-2);
}

优化版的实现方式，时间复杂度为O(n)

int fibonacci(int first, int second, int n) {
    if (n <= 0) {
        return 0;
    }
    if (n < 3) {
        return 1;
    }
    else if (n == 3) {
        return first + second;
    }
    else {
        return fibonacci(second, first + second, n - 1);
    }
}

递归算法的空间复杂度 = 每次递归的空间复杂度 * 递归深度

//递归实现二分法
int binary_search( int arr[], int l, int r, int x) {
    if (r >= l) {
        int mid = l + (r - l) / 2;
        if (arr[mid] == x)
            return mid;
        if (arr[mid] > x)
            return binary_search(arr, l, mid - 1, x);
        return binary_search(arr, mid + 1, r, x);
    }
    return -1;
}

二分法的时间复杂度是O(log(n)),空间复杂度为每次递归的空间复杂度 * 递归深度，

如果是拷贝地址，则每一层递归都是公用一块数组地址空间的，所以每次递归的空间复杂度是常数即：O(1)，空间复杂度为O(log(n)).
如果是拷贝值，则每一层递归都调用n个地址，所以每次递归的空间复杂度是常数即：O(n)，空间复杂度为O(nlog(n)).

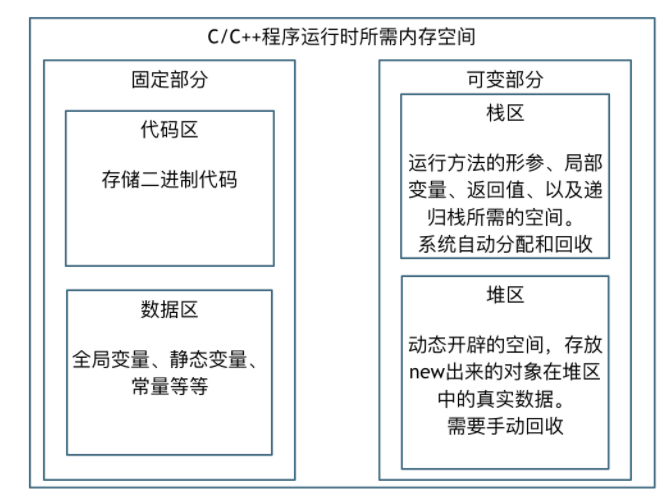
代码的内存消耗

不同的编程语言各自的内存管理方式。

1. C/C++这种内存堆空间的申请和释放完全靠自己管理
2. Java 依赖JVM来做内存管理，不了解jvm内存管理的机制，很可能会因一些错误的代码写法而导致内存泄漏或内存溢出
3. Python内存管理是由私有堆空间管理的，所有的python对象和数据结构都存储在私有堆空间中。程序员没有访问堆的权限，只有解释器才能操作，所以python的基本数据类型所用的内存会要远大于存放纯数据类型所占的内存，例如，我们都知道存储int型数据需要四个字节，但是使用Python 申请一个对象来存放数据的话，所用空间要远大于四个字节。

安装64位的操作系统的计算机内存都已经超过了4G，也就是指针大小如果还是4个字节的话，就已经不能寻址全部的内存地址，所以64位编译器使用8个字节的指针才能寻找所有的内存地址。

内存对齐

内存对齐的作用：以更多的空间为代价换取时间的快速。

struct node{
   int num;
   char cha;
}st;
int main() {
    int a[100];
    char b[100];
    cout << sizeof(int) << endl;
    cout << sizeof(char) << endl;
    cout << sizeof(a) << endl;
    cout << sizeof(b) << endl;
    cout << sizeof(st) << endl;
}

输出结果为：4，1，400，100，8

结构中的int和char就是内存对齐，如果不对齐，需要两次寻址和一次合并的操作。