字数统计: 4k字   |   阅读时长: 20分

二叉树(2)

101. 对称二叉树 - 力扣（LeetCode） (leetcode-cn.com)

给你一个二叉树的根节点 root ， 检查它是否轴对称。

递归法：

1.首先确定递归的参数是两个子树节点，返回值是bool类型。

2.确定中止条件

  • 左节点为空，右节点不为空，不对称，return false

  • 左不为空，右为空，不对称 return false

  • 左右都为空，对称，return true

  • 左右都不为空，比较节点数值，不相同就return false

3.确定单层递归的逻辑，即比较子树外侧节点和内侧节点，如果有一个不一样就返回false，否则返回true

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool compare(TreeNode* left, TreeNode* right)
    {
        if(left == NULL && right !=  NULL) return false;
        else if(left != NULL && right == NULL) return false;
        else if(left == NULL && right == NULL) return true;
        else if(left->val != right->val) return false;
        //以上条件都不满足就是这两个节点对称, 此时继续做递归
        bool outside = compare(left->left, right->right);
        bool inside = compare(left->right, right->left);
        bool isSame = outside && inside;
        return isSame;
    }
    bool isSymmetric(TreeNode* root) 
    {
        if(root == NULL) return true;
        return compare(root->left, root->right);
    }
};

迭代法：

用队列或者栈处理节点，判断的逻辑和递归相同。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool isSymmetric(TreeNode* root) 
    {
        if(root == NULL) return true;
        queue <TreeNode*> que;
        que.push(root->left);
        que.push(root->right);
        while(!que.empty())
        {
            TreeNode* leftNode = que.front();  que.pop();
            TreeNode* rightNode = que.front();  que.pop();
            if(!leftNode && !rightNode) continue;
            if(!leftNode || !rightNode || leftNode->val !=rightNode->val) return false;
            que.push(leftNode->left);
            que.push(rightNode->right);
            que.push(leftNode->right);
            que.push(rightNode->left);
        }
        return true;
    }
};

100. 相同的树 - 力扣（LeetCode） (leetcode-cn.com)

给你两棵二叉树的根节点 p 和 q ，编写一个函数来检验这两棵树是否相同。

如果两个树在结构上相同，并且节点具有相同的值，则认为它们是相同的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
//递归法
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool isSameTree(TreeNode* p, TreeNode* q) {
        if(p == NULL && q == NULL) return true;
        else if(p == NULL || q == NULL || p->val != q->val) return false;
        else return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
//迭代法
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool isSameTree(TreeNode* p, TreeNode* q) {
        if(p == NULL && q == NULL) return true;
        else if(p == NULL || q == NULL) return false; 
        queue <TreeNode*> que;
        que.push(p);
        que.push(q);
        while(!que.empty())
        {
            TreeNode* leftNode = que.front();  que.pop();
            TreeNode* rightNode = que.front();  que.pop();
            if(!leftNode && !rightNode) continue;
            if(!leftNode || !rightNode || leftNode->val !=rightNode->val) return false;
            que.push(leftNode->left);
            que.push(rightNode->left);
            que.push(leftNode->right);
            que.push(rightNode->right);
        }
        return true;
    }
};

递归方法也是深度优先搜索，迭代法也是广度优先搜索。

572. 另一棵树的子树 - 力扣（LeetCode） (leetcode-cn.com)

给你两棵二叉树 root 和 subRoot 。检验 root 中是否包含和 subRoot 具有相同结构和节点值的子树。如果存在，返回 true ；否则，返回 false 。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool compare(TreeNode* left, TreeNode* right)
    {
        if(left == NULL && right !=  NULL) return false;
        else if(left != NULL && right == NULL) return false;
        else if(left == NULL && right == NULL) return true;
        else if(left->val != right->val) return false;
        //以上条件都不满足就是这两个节点对称, 此时继续做递归
        bool outside = compare(left->left, right->left);
        bool inside = compare(left->right, right->right);
        bool isSame = outside && inside;
        return isSame;
    }
    bool isSubtree(TreeNode* root, TreeNode* subRoot) {
        if(root == NULL) return false;
        if(subRoot == NULL) return true;
        //要不是其本身，要不是左子树，要不是右子树
        else return compare(root, subRoot) || isSubtree(root->left, subRoot) || isSubtree(root->right, subRoot);
    }
};

思路：递归法

  1. Compare函数用于递归检查需要判断的树对应结点是否相同；（内层递归检查函数）
  2. isSubtree函数则用于判断是否为子树；（外层递归判断函数）

104. 二叉树的最大深度 - 力扣（LeetCode） (leetcode-cn.com)

递归法：后序遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int maxDepth(TreeNode* root) {
        if(root == NULL) return 0;
        int leftDepth = maxDepth(root->left);
        int rightDepth = maxDepth(root->right);
        return max(leftDepth, rightDepth) + 1;
    }
};

迭代法：层序遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int maxDepth(TreeNode* root) {
        if(root == NULL) return 0;
        int depth = 0;
        queue <TreeNode*> que;
        if(root != NULL) que.push(root);
        while(!que.empty())
        {
            depth++;
            int size = que.size();
            for(int i = 0; i < size; i++)
            {
                TreeNode* node = que.front();
                que.pop();
                if(node->left != NULL) que.push(node->left);
                if(node->right != NULL) que.push(node->right);
            }
        }
        return depth;

559. N 叉树的最大深度 - 力扣（LeetCode） (leetcode-cn.com)

相同的思路，就是左右孩子换成了多个孩子节点。

递归法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
/*
// Definition for a Node.
class Node {
public:
    int val;
    vector<Node*> children;

    Node() {}

    Node(int _val) {
        val = _val;
    }

    Node(int _val, vector<Node*> _children) {
        val = _val;
        children = _children;
    }
};
*/

class Solution {
public:
    int maxDepth(Node* root) {
        if(root == 0)   return 0;
        int depth = 0;
        for(int i = 0; i < root->children.size(); i++)
        depth = max(depth, maxDepth(root->children[i]));
        return depth + 1;
    }
};

迭代法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
/*
// Definition for a Node.
class Node {
public:
    int val;
    vector<Node*> children;

    Node() {}

    Node(int _val) {
        val = _val;
    }

    Node(int _val, vector<Node*> _children) {
        val = _val;
        children = _children;
    }
};
*/

class Solution {
public:
    int maxDepth(Node* root) {
        if(root == 0)   return 0;
        queue <Node*> que;
        que.push(root);
        int depth = 0;
        while(!que.empty())
        {
            depth++;
            int size = que.size();
            for(int i = 0; i < size; i++)
            {
                Node* node = que.front();
                que.pop();
                for(int j = 0; j < node->children.size(); j++)
                {
                    que.push(node->children[j]);
                }
            }
        }
        return depth;
    }
};

111. 二叉树的最小深度 - 力扣（LeetCode） (leetcode-cn.com)

给定一个二叉树，找出其最小深度。

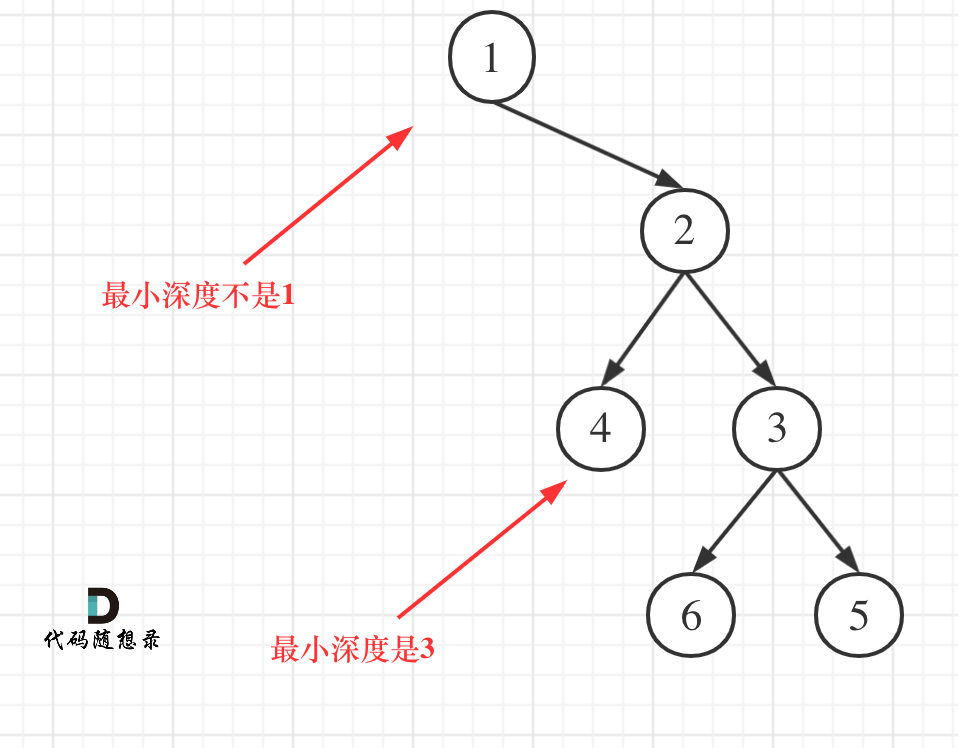
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

说明：叶子节点是指没有子节点的节点。

递归法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int minDepth(TreeNode* root) {
        if(root == NULL) return 0;
        int leftDepth = minDepth(root->left);
        int rightDepth = minDepth(root->right);
        if(root->left == NULL && root->right != NULL)
        return 1 + rightDepth; //由于是到叶子节点, 因此过根节点不算
        if(root->left != NULL && root->right == NULL)
        return 1 + leftDepth;
        int result = min(leftDepth, rightDepth) + 1;
        return result;
    }
};

这里特别要注意题里要求最小深度必须世道叶子节点，因此和求最大深度的递归逻辑有一点区别。

迭代法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int minDepth(TreeNode* root) {
        if(root == NULL) return 0;
        int depth = 0;
        queue <TreeNode*> que;
        if(root != NULL) que.push(root);
        while(!que.empty())
        {
            depth++;
            int size = que.size();
            for(int i = 0; i < size; i++)
            {
                TreeNode* node = que.front();
                que.pop();
                if(node->left != NULL) que.push(node->left);
                if(node->right != NULL) que.push(node->right);
                if(node->left == NULL && node->right == NULL)
                return depth; 
            }
        }
        return depth;
    }
};

注意迭代法是当节点左右孩子都为空时为叶子节点，此时返回树的深度。

222. 完全二叉树的节点个数 - 力扣（LeetCode） (leetcode-cn.com)

给你一棵 完全二叉树 的根节点 root ，求出该树的节点个数。

完全二叉树 的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2^(h - 1) 个节点。

思路

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
//方法1：按普通的二叉树处理，层序遍历(迭代法)，时间复杂度是O(n),空间复杂度也是O(n)
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int countNodes(TreeNode* root) {
        queue <TreeNode*> que;
        if(root != NULL)    que.push(root);
        int sum = 0;
        while(!que.empty())
        {
            sum++;
            TreeNode* node = que.front();
            que.pop();
            if(node->left != NULL) que.push(node->left);
            if(node->right != NULL) que.push(node->right);
        }
        return sum;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
//递归法，时间复杂度是O(n),空间复杂度也是O(logn)
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int countNodes(TreeNode* root) {
        if(root == NULL)    return 0;
        else
        return 1 + countNodes(root->left) + countNodes(root->right);
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
//针对完全二叉树的特殊解法，递归法，时间复杂度：$O(\log n × \log n)$空间复杂度：$O(\log n)$
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int countNodes(TreeNode* root) {
        if(root == NULL)    return 0;
        TreeNode* left = root->left;
        TreeNode* right = root->right;
        int leftHeight = 0, rightHeight = 0;
        while(left != NULL) //注意这里是判断left为不为空，相当于多循环了一次，所以前面的leftHeight为0
        {
            left = left->left;
            leftHeight++;
        }
        while(right != NULL)
        {
            right = right->right;
            rightHeight++;
        }
        if(leftHeight == rightHeight)
        return (2 << leftHeight) - 1;//左移leftHeight，相当于2^leftHeight
        return countNodes(root->left) + countNodes(root->right) + 1;
    }
};
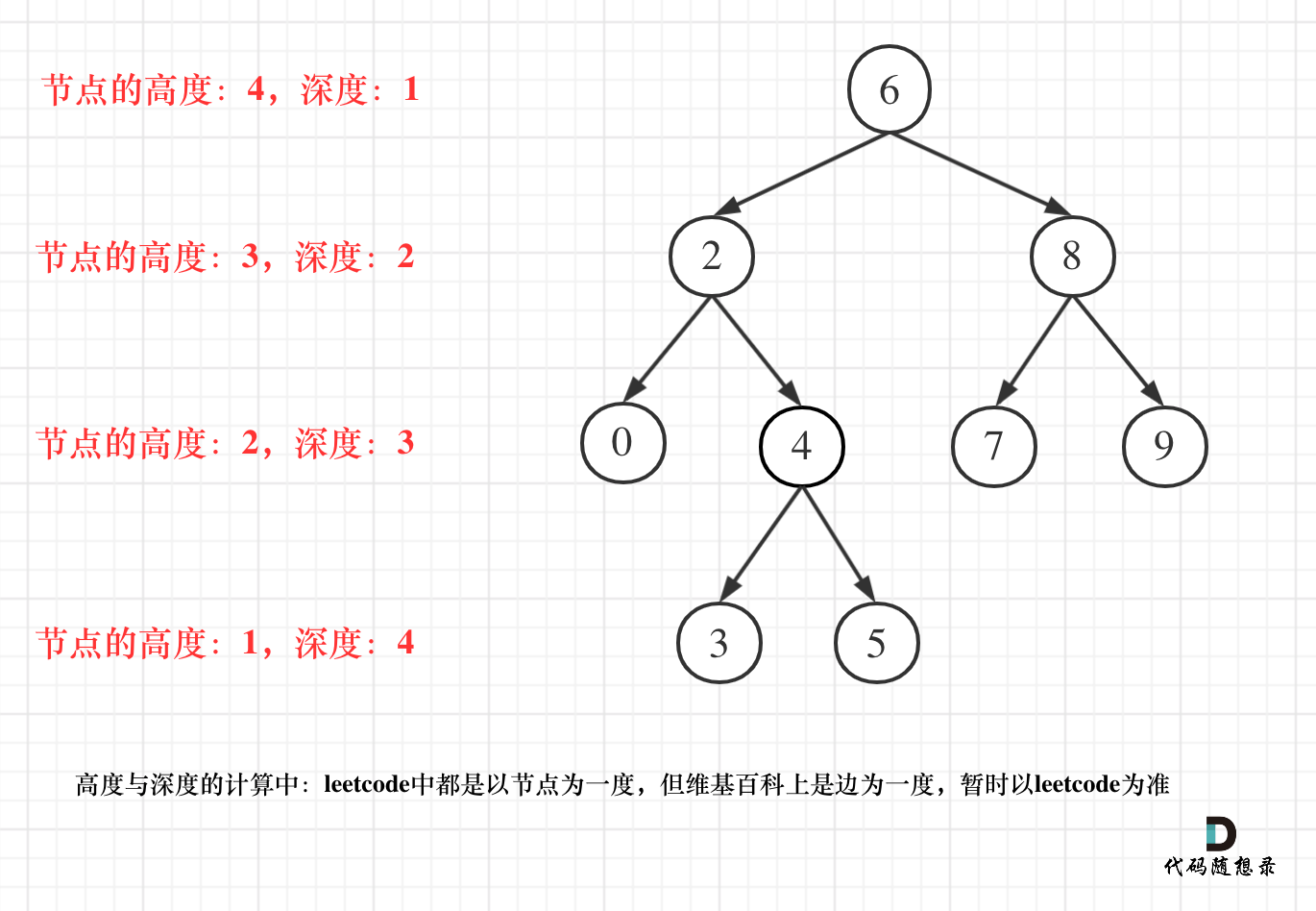
  • 二叉树节点的深度：指从根节点到该节点的最长简单路径边的条数，理论上用先序遍历。
  • 二叉树节点的高度：指从该节点到叶子节点的最长简单路径边的条数，理论上用后序遍历，后序遍历也就是递归。

110. 平衡二叉树 - 力扣（LeetCode） (leetcode-cn.com)

给定一个二叉树，判断它是否是高度平衡的二叉树。

本题中，一棵高度平衡二叉树定义为：

一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
//递归法
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int getHeight(TreeNode* node)
    {
        if(node == NULL)    return 0;
        int leftHeight = getHeight(node->left);
        if(leftHeight == -1)    return -1;
        int rightHeight = getHeight(node->right);
        if(rightHeight == -1)   return -1;
        return abs(leftHeight - rightHeight) > 1? -1 : 1 + max(leftHeight, rightHeight);
    }
    bool isBalanced(TreeNode* root) {
        if(getHeight(root) == -1)
        return false;
        else
        return true; 
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
//迭代法，后序遍历求高度，了解
class Solution {
private:
    int getDepth(TreeNode* cur) {
        stack<TreeNode*> st;
        if (cur != NULL) st.push(cur);
        int depth = 0; // 记录深度
        int result = 0;
        while (!st.empty()) {
            TreeNode* node = st.top();
            if (node != NULL) {
                st.pop();
                st.push(node);                          // 中
                st.push(NULL);
                depth++;
                if (node->right) st.push(node->right);  // 右
                if (node->left) st.push(node->left);    // 左

            } else {
                st.pop();
                node = st.top();
                st.pop();
                depth--;
            }
            result = result > depth ? result : depth;
        }
        return result;
    }

public:
    bool isBalanced(TreeNode* root) {
        stack<TreeNode*> st;
        if (root == NULL) return true;
        st.push(root);
        while (!st.empty()) {
            TreeNode* node = st.top();                       // 中
            st.pop();
            if (abs(getDepth(node->left) - getDepth(node->right)) > 1) {
                return false;
            }
            if (node->right) st.push(node->right);           // 右（空节点不入栈）
            if (node->left) st.push(node->left);             // 左（空节点不入栈）
        }
        return true;
    }
};

如果是模拟前中后序遍历就用栈，如果是适合层序遍历就用队列，当然还是其他情况，那么就是 先用队列试试行不行，不行就用栈。

257. 二叉树的所有路径 - 力扣（LeetCode） (leetcode-cn.com)

给你一个二叉树的根节点 root ，按 任意顺序 ，返回所有从根节点到叶子节点的路径。

叶子节点 是指没有子节点的节点。

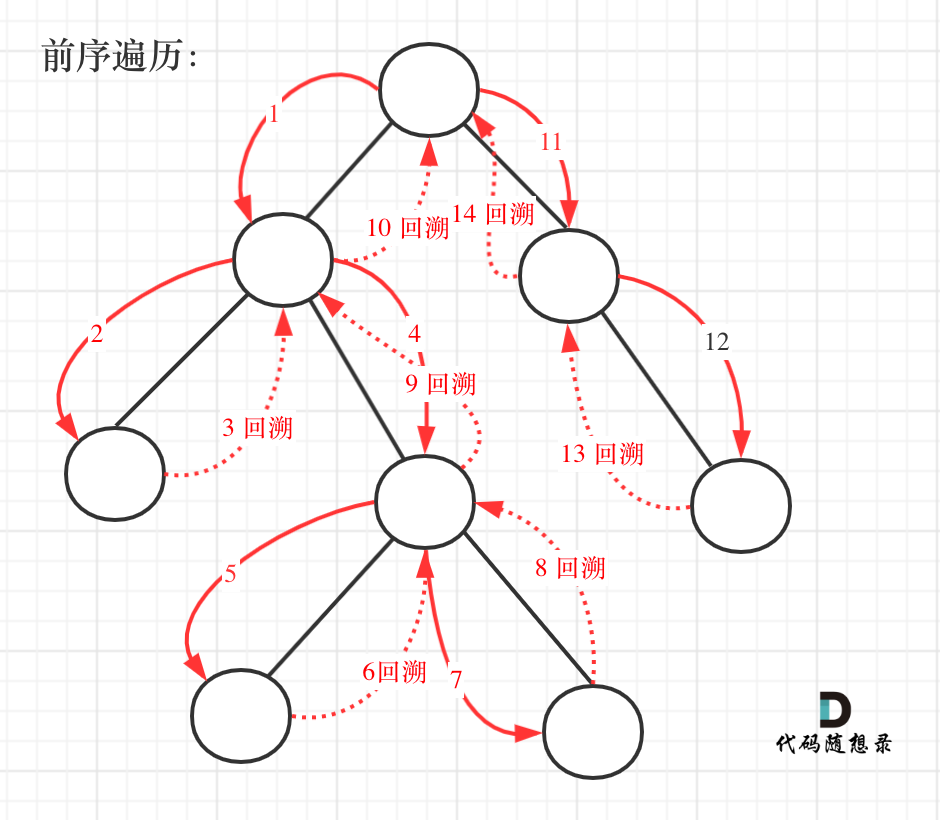
本题应该用先序遍历，而且涉及到了回溯。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
private:
    void tranversal(TreeNode* cur, vector <int> &path, vector <string> &result)
    {
        path.push_back(cur->val);
        if(cur->left == NULL && cur->right == NULL)
        {
            string sPath;
            for(int i = 0; i < path.size() - 1; i++)
            {
            sPath = sPath + to_string(path[i]);
            sPath = sPath + "->";
            }
            sPath = sPath + to_string(path[path.size() - 1]);
            result.push_back(sPath);
            return; //return不带返回值，应用于void，相当于break。
        }
        if(cur->left != NULL)
        {
            tranversal(cur->left, path, result);
            path.pop_back(); //回溯
        }
        if(cur->right != NULL)
        {
            tranversal(cur->right, path, result);
            path.pop_back();
        }
    }
public:
    vector<string> binaryTreePaths(TreeNode* root) {
        vector <string> result;
        vector <int> path;
        if(root == NULL)    return result;
        tranversal(root, path, result);
        return result;
    }
};

path.pop_back();体现回溯的思想

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Solution {
private:

    void traversal(TreeNode* cur, string path, vector<string>& result) {
        path += to_string(cur->val); // 中
        if (cur->left == NULL && cur->right == NULL) {
            result.push_back(path);
            return;
        }
        if (cur->left) traversal(cur->left, path + "->", result); // 左
        if (cur->right) traversal(cur->right, path + "->", result); // 右
        /*
        if (cur->left) {
        path += "->"; 
        traversal(cur->left, path, result); 			 
        path.pop_back(); path.pop_back(); }// 左,需要pop两次是因为->是两个字符
        if (cur->right) {
        path += "->"; 
        traversal(cur->right, path, result); 
        path.pop_back();path.pop_back();}// 右
        */
    }

public:
    vector<string> binaryTreePaths(TreeNode* root) {
        vector<string> result;
        string path;
        if (root == NULL) return result;
        traversal(root, path, result);
        return result;

    }
};

如上代码精简了不少，也隐藏了不少东西。

注意在函数定义的时候void traversal(TreeNode* cur, string path, vector<string>& result) ，定义的是string path，每次都是复制赋值，不用使用引用，否则就无法做到回溯的效果。如果是引用相当于修改的是同一个对象，这样就把原来的path改变了。

回溯隐藏在traversal(cur->left, path + "->", result);中的 path + "->"。 每次函数调用完，path依然是没有加上”->” 的，这就是回溯了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<string> binaryTreePaths(TreeNode* root) {
        stack <TreeNode*> treeSt;// 保存树的遍历节点
        stack <string> pathSt;   // 保存遍历路径的节点
        vector <string> result;  // 保存最终路径集合
        if(root == NULL)    return result;
        treeSt.push(root);
        pathSt.push(to_string(root->val));
        while(!treeSt.empty())
        {
            TreeNode* node = treeSt.top();
            treeSt.pop();
            string path = pathSt.top();
            pathSt.pop();
            if(node->left == NULL && node->right == NULL)
            {
                result.push_back(path);
            }
            if(node->right != NULL) 
            {
                treeSt.push(node->right);  
                pathSt.push(path + "->" + to_string(node->right->val));
            }
            if(node->left != NULL)
            {
                treeSt.push(node->left);
                pathSt.push(path + "->" + to_string(node->left->val));
            }
        }
        return result;
    }
};

迭代法，就是一个前序遍历，比较好理解。

扫一扫，分享到微信

微信分享二维码
本站总访问量次 |

tag:

    缺失模块。
    1、请确保node版本大于6.2
    2、在博客根目录（注意不是yilia根目录）执行以下命令：
    npm i hexo-generator-json-content --save

    3、在根目录_config.yml里添加配置： 

      jsonContent:
    meta: false
    pages: false
    posts:
      title: true
      date: true
      path: true
      text: false
      raw: false
      content: false
      slug: false
      updated: false
      comments: false
      link: false
      permalink: false
      excerpt: false
      categories: false
      tags: true

这一定是一个<br><br>很长很长的一生啊