字数统计: 2.6k字   |   阅读时长: 14分

手写数字识别

手写数字识别(CS229 ex3)

首先确定这个问题是一个分类问题。

  • 数据(data)的结构：
    • X的维度是5000*400，其中5000是数字的总个数，400是数据的像素点是20*20的；y的维度是5000*1, 存的是数据对应的真实值；
    • sample_idx是从data中选取了100个数字，sample_images是这100个数字的像素值；

  • sigmoid函数：可以将一个实数映射为一个（0，1）区间内的数；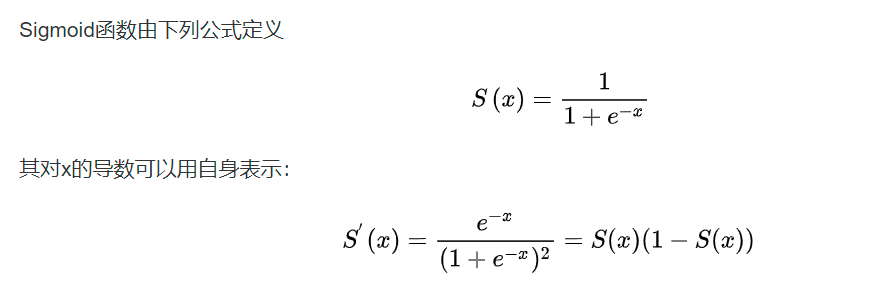

    image-20220307223032066

优点：平滑、易于求导。

缺点：激活函数计算量大，反向传播求误差梯度时，求导涉及除法；反向传播时，很容易就会出现梯度消失的情况，从而无法完成深层网络的训练。

1
2
3
#定义sigmoid函数
def sigmoid(z):
    return 1 / (1 + np.exp(-z))

  • 代价函数

希望代价函数是一个凸函数，而不是具有多个局部最优解。

image-20220308153911452

根据此思想，可以定义代价函数如下：

1
2
3
4
5
6
7
def costReg(theta, X, y, lamda):
    n = len(theta)
    m = len(y)
    first = -y * np.log(sigmoid(X @ theta.reshape(n,1)))
    second = -(1 - y) * np.log(1 - sigmoid(X @ theta.reshape(n,1)))
    reg = (lamda / (2 * m)) * np.sum(np.power(theta.reshape(n,1), 2)) #lamda是学习率
    return (sum(first + second) / m) + reg

正则化方法：L1和L2 regularization、数据集扩增、dropout - bonelee - 博客园 (cnblogs.com)

reg表示正则化，在代价函数的后面加一个常数项，减小每个数据的权重，防止过拟合，注意正则化不包括theta0

梯度下降算法_梯度下降算法中的偏导公式推导_weixin_39882948的博客-CSDN博客

梯度函数的计算本质上就是对代价函数求偏导

1
2
3
4
5
6
7
8
def gradientReg_noLoop(theta, X, y, lamda):
    n = len(theta)
    m = len(y)
    error = sigmoid(X @ theta.reshape(n, 1)) - y
    grad = (X.T @ error / m) + ((lamda / m) * theta.reshape(n, 1))
    grad[0][0] = np.sum(error * X[:, 0].reshape(m, 1)) / m
    grad = np.reshape(grad, (n,))
    return grad

然后就是对数据进行分类，分类函数为：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# 分类函数
def one_vs_all(theta, X, y, lamda):
    m = len(y)
    n = len(theta[0])
    # 从 1 到 10 总共训练 10 个分类器，依次保存到 theta
    for i in range(1, 11):
        # label 为 i 置 1，不为 i 置 0
        y_i = np.array([1 if label == i else 0 for label in y])
        y_i = np.reshape(y_i,(m, 1))
        theta_i = theta[i,:]
        theta_i = np.reshape(theta_i,(n, 1))
        # 使用 scipy 的库函数就算最优参数
        result = opt.fmin_tnc(func=costReg, x0=theta_i, fprime=gradientReg_noLoop, args=(X, y_i, lamda))
        #print(result)
        # 保存第 i 个分类器,theta[i]对应数字为i训练对应的theta值
        theta[i,:] = result[0]
        #print(theta)

特别注意：区分矩阵点乘 @ 和矩阵乘法 * ，写错的话可能会导致难以 debug 的错误！！！

最后是对数据进行测试：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# 测试函数
def predict_all(theta, X, y):
    m = len(y)
    y_pre = np.zeros((m, 2))
    # term 为 m * 10 的数组，每一行依次记录该样本为 1，2，……，9，0 的概率
    term = sigmoid(X @ theta.T)
    # 选取最大概率对应的 label 作为预测结果
    for sample in range(m):
        for i in range(1, 11):
            if(term[sample][i] > y_pre[sample][1]): #找到可能概率最大的那个数字
                y_pre[sample][0] = i #记录当前数字对应概率最大的分类
                y_pre[sample][1] = term[sample][i] #记录当前数字对应的最大概率的值
    rate = 0.0
    for sample in range(m):
        if(y_pre[sample][0] == y[sample]):#如果预测值和真实值一样
            rate += 1
    rate = (rate / m) * 100
    print('accuracy = {0}%'.format(rate))

主函数部分：

1
2
3
4
5
data = loadData('ex3data1.mat')
#fig = plot()
X, y, theta = initData(data)
one_vs_all(theta, X, data['y'], 0)
predict_all(theta, X, data['y'])

学习率为 0 时训练结果：accuracy = 97.26%

学习率为 0.5 时训练结果：accuracy = 95.1%

卷积神经网络：已经给了训练的theta，包括theta1和theta2；

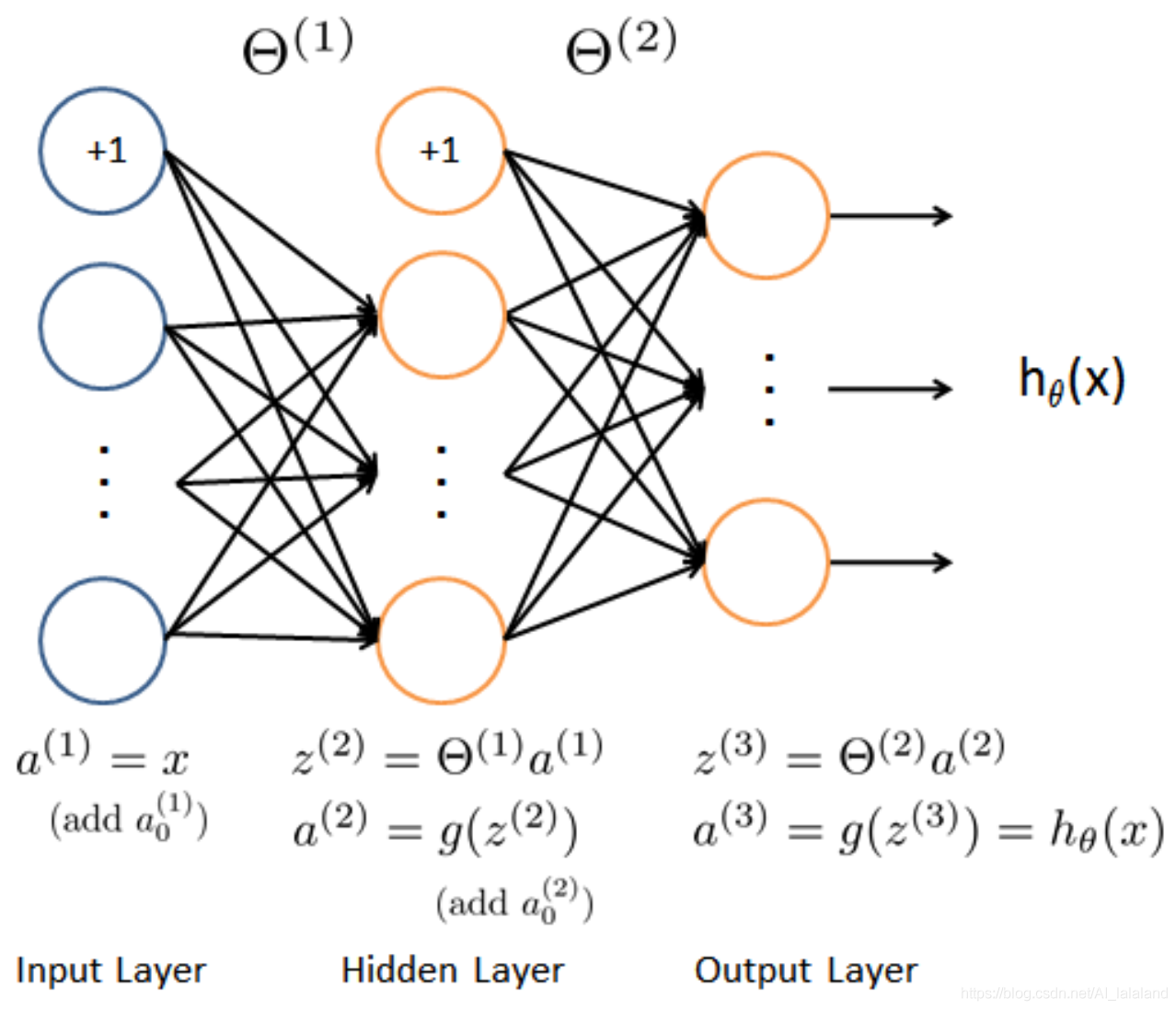
根据神经网络的结构（一层输入层 400+1 ，一层隐藏层 25+1 ，一层输出层 10），计算结果：

theta1的维度是(25, 401)，theta2的维度是(10, 26)

前向传播算法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
# -*- coding: utf-8 -*-
"""
Created on Tue Mar  8 17:12:12 2022

@author: 李政翰
"""

import numpy as np
import matplotlib
import matplotlib.pyplot as plt
from scipy.io import loadmat
 
def loadData(filename):
    return loadmat(filename)
 
def initData(data):
    X = data['X']
    # X : 增加一列 bias（要增加到第一列）
    X = np.insert(X, 0, values=np.ones(X.shape[0]), axis=1)
    y = data['y']
    return X, y
 
def sigmoid(z):
    return 1 / (1 + np.exp(-z))
 
def NN(X, theta1, theta2):
    hidden_layer = sigmoid(X @ theta1.T)
    hidden_layer = np.insert(hidden_layer, 0, values=np.ones(X.shape[0]), axis=1)
    output = sigmoid(hidden_layer @ theta2.T)
    return output
 
def predict(output, y):
    m = len(y)
    rate = 0.0
    for sample in range(m):
        pre_res = -1
        pre_pro = 0.0
        for i in range(10):
            if(output[sample][i] > pre_pro):
                pre_res = i + 1
                pre_pro = output[sample][i]
        if(pre_res == y[sample]):
            rate += 1
        #print(pre_res)
    rate = (rate / m) * 100
    print('accuracy = {0}%'.format(rate))
 
def visualizing(layer):
    sample_idx = range(0,5000,50)
    sample_images = layer[sample_idx, :]
    fig, ax_array = plt.subplots(nrows=10, ncols=10, sharey=True, sharex=True, figsize=(8, 8))
    for r in range(10):
        for c in range(10):
            ax_array[r, c].matshow(sample_images[10 * r + c].reshape((5, 5)).T,cmap=matplotlib.cm.binary)
            plt.xticks(np.array([]))
            plt.yticks(np.array([]))
    plt.show()
   
data = loadData('ex3data1.mat')
X, y = initData(data)
theta = loadData('ex3weights.mat')
theta1 = theta['Theta1']
theta2 = theta['Theta2']
output = NN(X, theta1, theta2)
predict(output, y)

神经网络和反向传播算法：

image-20220310234326584

首先要明白一点，BP 做的事情是求代价函数 J 对参数 theta (也可以用 weight 表示)的偏导数，根据链式法则，表示如下：

吴恩达机器学习CS229A_EX4_神经网络与反向传播算法_Python3_AI_lalaland的博客-CSDN博客

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
# -*- coding: utf-8 -*-
"""
Created on Tue Aug 10 16:26:34 2021

@author: 李政翰
"""


import numpy as np 
#import pandas as pd 
import matplotlib.pyplot as plt 
import matplotlib 
from scipy.io import loadmat 
from sklearn.preprocessing import OneHotEncoder
np.seterr(divide='ignore',invalid='ignore')

data = loadmat('F:/学习资料/大三上/机器学习/Coursera斯坦福ML/python_hw/ex4/ex4data1.mat')
#print(data) 

#可视化数据输出
sample_idx = np.random.choice(np.arange(data['X'].shape[0]), 100)
sample_images = data['X'][sample_idx, :]
#print(sample_images)

#fig, ax_array = plt.subplots(nrows=10, ncols=10, sharey=True, sharex=True, figsize=(12, 12))
#for r in range(10):
#    for c in range(10):
#        ax_array[r, c].matshow(np.array(sample_images[10 * r + c].reshape((20, 20))).T,cmap=matplotlib.cm.binary)
#        plt.xticks(np.array([]))
#        plt.yticks(np.array([])) 
        
#前向传播算法和代价函数
def sigmoid(z):
    return 1 / (1 + np.exp(-z))
        
# 前向传播函数
def forward_propagate(X, theta1, theta2):
    m = X.shape[0]
    a1 = np.insert(X, 0, values=np.ones(m), axis=1)
    z2 = a1 * theta1.T
    a2 = np.insert(sigmoid(z2), 0, values=np.ones(m), axis=1)
    z3 = a2 * theta2.T
    h = sigmoid(z3)
    return a1, z2, a2, z3, h

def cost(theta1, theta2 , input_size, hidden_size, num_labels, X, y, learning_rate):
    m = X.shape[0]
    X = np.matrix(X)
    y = np.matrix(y)
    
    # 计算前向传播的各项参数
    a1, z2, a2, z3, h = forward_propagate(X, theta1, theta2)
    
    # 计算代价函数
    J = 0
    for i in range(m):
        first_term = np.multiply(-y[i,:], np.log(h[i,:]))
        second_term = np.multiply((1 - y[i,:]), np.log(1 - h[i,:]))
        J += np.sum(first_term - second_term)
    J = J / m
    return J

rows = data['X'].shape[0]
params = data['X'].shape[1]
#y = np.array([1 if label == 0 else 0 for label in data['y']])
#y = np.reshape(y, (rows, 1))

encoder = OneHotEncoder(sparse=False)
y_onehot = encoder.fit_transform(data['y'])
#print(y_onehot.shape)

# 初始化设置
input_size = 400
hidden_size = 25
num_labels = 10
learning_rate = 1
weight = loadmat("F:/学习资料/大三上/机器学习/Coursera斯坦福ML/python_hw/ex4/ex4weights.mat")
theta1, theta2 = weight['Theta1'], weight['Theta2']
#print(theta1.shape, theta2.shape)
X = np.matrix(data['X'])


#print(cost(theta1, theta2, input_size, hidden_size, num_labels, X, y_onehot, learning_rate))

#正则化代价函数
def costReg(theta1, theta2, input_size, hidden_size, num_labels, X, y, learning_rate):
    m = X.shape[0]
    X = np.matrix(X)
    y = np.matrix(y)
    # run the feed-forward pass
    a1, z2, a2, z3, h = forward_propagate(X, theta1, theta2)
    # compute the cost
    J = 0
    for i in range(m):
        first_term = np.multiply(-y[i,:], np.log(h[i,:]))
        second_term = np.multiply((1 - y[i,:]), np.log(1 - h[i,:]))
        J += np.sum(first_term - second_term)
    J = J / m
    # add the cost regularization term
    J += (float(learning_rate) / (2 * m)) * (np.sum(np.power(theta1[:,1:], 2)) + np.sum(np.power(theta2[:,1:], 2)))
    return J

#print(costReg(theta1, theta2, input_size, hidden_size, num_labels, X, y_onehot, learning_rate))

#sigmoid梯度
def sigmoid_gradient(z):
    return np.multiply(sigmoid(z), (1 - sigmoid(z)))

#print(sigmoid_gradient(0))

#初始随机
params = (np.random.random(size=hidden_size * (input_size + 1) + num_labels * (hidden_size + 1)) - 0.5) * 0.24 #维数是25*401 + 1 * 26

#反向传播
def backprop(params, input_size, hidden_size, num_labels, X, y, learning_rate):
    m = X.shape[0]
    X = np.matrix(X)
    y = np.matrix(y)
    theta1, theta2 = weight['Theta1'], weight['Theta2']
    # run the feed-forward pass
    a1, z2, a2, z3, h = forward_propagate(X, theta1, theta2)
    
    # reshape the parameter array into parameter matrices for each layer
    theta1 = np.matrix(np.reshape(params[:hidden_size * (input_size + 1)], (hidden_size, (input_size + 1))))
    theta2 = np.matrix(np.reshape(params[hidden_size * (input_size + 1):], (num_labels, (hidden_size + 1))))
    
    # initializations
    J = 0
    delta1 = np.zeros(theta1.shape)  # (25, 401)
    delta2 = np.zeros(theta2.shape)  # (10, 26)
    
    # compute the cost
    for i in range(m):
        first_term = np.multiply(-y[i,:], np.log(h[i,:]))
        second_term = np.multiply((1 - y[i,:]), np.log(1 - h[i,:]))
        J += np.sum(first_term - second_term)
    
    J = J / m

    # perform backpropagation
    for t in range(m):
        a1t = a1[t,:]  # (1, 401)
        z2t = z2[t,:]  # (1, 25)
        a2t = a2[t,:]  # (1, 26)
        ht = h[t,:]  # (1, 10)
        yt = y[t,:]  # (1, 10)
        
        d3t = ht - yt  # (1, 10)
        
        z2t = np.insert(z2t, 0, values=np.ones(1))  # (1, 26)
        d2t = np.multiply((theta2.T * d3t.T).T, sigmoid_gradient(z2t))  # (1, 26)
        
        delta1 = delta1 + (d2t[:,1:]).T * a1t
        delta2 = delta2 + d3t.T * a2t
        
    delta1 = delta1 / m
    delta2 = delta2 / m
    
    return J, delta1, delta2

#梯度校验

#正则化神经网络
def backpropReg(params, input_size, hidden_size, num_labels, X, y, learning_rate):
    m = X.shape[0]
    X = np.matrix(X)
    y = np.matrix(y)
    
    # reshape the parameter array into parameter matrices for each layer
    theta1 = np.matrix(np.reshape(params[:hidden_size * (input_size + 1)], (hidden_size, (input_size + 1))))
    theta2 = np.matrix(np.reshape(params[hidden_size * (input_size + 1):], (num_labels, (hidden_size + 1))))
    
    # run the feed-forward pass
    a1, z2, a2, z3, h = forward_propagate(X, theta1, theta2)
    
    # initializations
    J = 0
    delta1 = np.zeros(theta1.shape)  # (25, 401)
    delta2 = np.zeros(theta2.shape)  # (10, 26)
    
    # compute the cost
    for i in range(m):
        first_term = np.multiply(-y[i,:], np.log(h[i,:]))
        second_term = np.multiply((1 - y[i,:]), np.log(1 - h[i,:]))
        J += np.sum(first_term - second_term)
    
    J = J / m
    
    # add the cost regularization term
    J += (float(learning_rate) / (2 * m)) * (np.sum(np.power(theta1[:,1:], 2)) + np.sum(np.power(theta2[:,1:], 2)))
    
    # perform backpropagation
    for t in range(m):
        a1t = a1[t,:]  # (1, 401)
        z2t = z2[t,:]  # (1, 25)
        a2t = a2[t,:]  # (1, 26)
        ht = h[t,:]  # (1, 10)
        yt = y[t,:]  # (1, 10)
        
        d3t = ht - yt  # (1, 10)
        
        z2t = np.insert(z2t, 0, values=np.ones(1))  # (1, 26)
        d2t = np.multiply((theta2.T * d3t.T).T, sigmoid_gradient(z2t))  # (1, 26)
        
        delta1 = delta1 + (d2t[:,1:]).T * a1t
        delta2 = delta2 + d3t.T * a2t
        
    delta1 = delta1 / m
    delta2 = delta2 / m
    
    # add the gradient regularization term
    delta1[:,1:] = delta1[:,1:] + (theta1[:,1:] * learning_rate) / m
    delta2[:,1:] = delta2[:,1:] + (theta2[:,1:] * learning_rate) / m
    
    # unravel the gradient matrices into a single array
    grad = np.concatenate((np.ravel(delta1), np.ravel(delta2)))
    
    return J, grad

from scipy.optimize import minimize

# minimize the objective function
fmin = minimize(fun=backpropReg, x0=(params), args=(input_size, hidden_size, num_labels, X, y_onehot, learning_rate), 
                method='TNC', jac=True, options={'maxiter': 250})
#print(fmin)

X = np.matrix(X)
thetafinal1 = np.matrix(np.reshape(fmin.x[:hidden_size * (input_size + 1)], (hidden_size, (input_size + 1))))
thetafinal2 = np.matrix(np.reshape(fmin.x[hidden_size * (input_size + 1):], (num_labels, (hidden_size + 1))))

a1, z2, a2, z3, h = forward_propagate(X, thetafinal1, thetafinal2 )
y_pred = np.array(np.argmax(h, axis=1) + 1)
#print(y_pred)

#from sklearn.metrics import classification_report#这个包是评价报告
#print(classification_report(data['y'], y_pred))

rate = 0.0
for i in range (rows):
    if(data['y'][i] == y_pred[i]):
        rate += 1
rate = (rate / rows) * 100
print('accuracy = {}%'.format(rate))

hidden_layer = thetafinal1[:, 1:] 
hidden_layer.shape

#fig, ax_array = plt.subplots(nrows=5, ncols=5, sharey=True, sharex=True, figsize=(12, 12))
#for r in range(5):
#    for c in range(5):
#        ax_array[r, c].matshow(np.array(hidden_layer[5 * r + c].reshape((20, 20))),cmap=matplotlib.cm.binary)
#        plt.xticks(np.array([]))
#        plt.yticks(np.array([]))

最终达到了accuracy = 99.16%

扫一扫，分享到微信

微信分享二维码
本站总访问量次 |

tag:

    缺失模块。
    1、请确保node版本大于6.2
    2、在博客根目录（注意不是yilia根目录）执行以下命令：
    npm i hexo-generator-json-content --save

    3、在根目录_config.yml里添加配置： 

      jsonContent:
    meta: false
    pages: false
    posts:
      title: true
      date: true
      path: true
      text: false
      raw: false
      content: false
      slug: false
      updated: false
      comments: false
      link: false
      permalink: false
      excerpt: false
      categories: false
      tags: true

这一定是一个<br><br>很长很长的一生啊