2022-05-15

字数统计: 4.5k字 | 阅读时长: 19分

动态规划-3

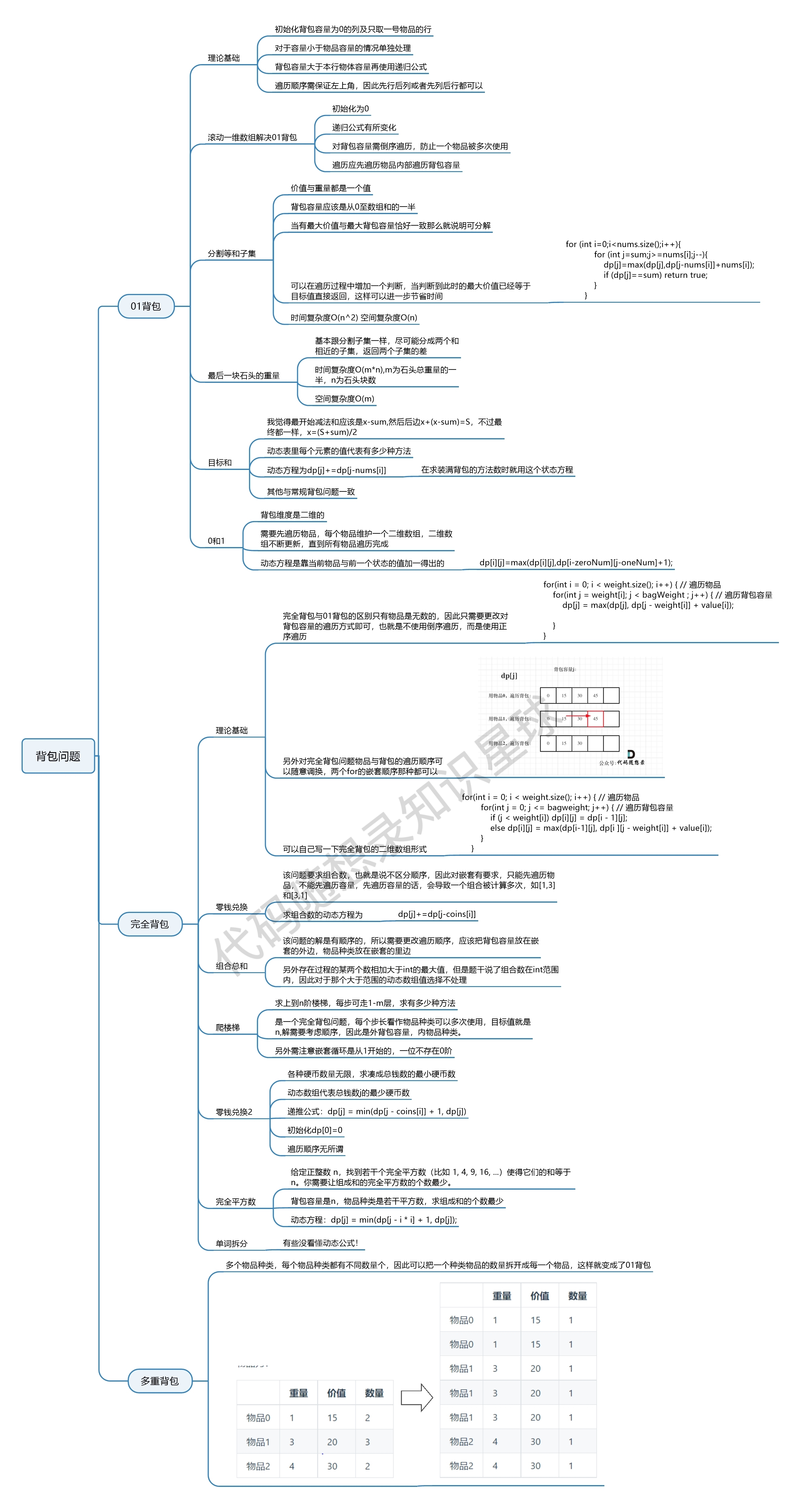
多重背包问题

有N种物品和一个容量为V 的背包。第i种物品最多有Mi件可用，每件耗费的空间是Ci ，价值是Wi 。求解将哪些物品装入背包可使这些物品的耗费的空间总和不超过背包容量，且价值总和最大。

多重背包和01背包是非常像的，为什么和01背包像呢？

每件物品最多有Mi件可用，把Mi件摊开，其实就是一个01背包问题了。

例如：背包最大重量为10。物品为：

	重量	价值	数量
物品0	1	15	2
物品1	3	20	3
物品2	4	30	2

问背包能背的物品最大价值是多少？和如下情况一样。

	重量	价值	数量
物品0	1	15	1
物品0	1	15	1
物品1	3	20	1
物品1	3	20	1
物品1	3	20	1
物品2	4	30	1
物品2	4	30	1

毫无区别，这就转成了一个01背包问题了，且每个物品只用一次。

//时间复杂度：O(m × n × k)，m：物品种类个数，n背包容量，k单类物品数量
void test_multi_pack() {
    vector<int> weight = {1, 3, 4};
    vector<int> value = {15, 20, 30};
    vector<int> nums = {2, 3, 2};
    int bagWeight = 10;
    for (int i = 0; i < nums.size(); i++) {
        while (nums[i] > 1) { // nums[i]保留到1，把其他物品都展开
            weight.push_back(weight[i]);
            value.push_back(value[i]);
            nums[i]--;
        }
    }

    vector<int> dp(bagWeight + 1, 0);
    for(int i = 0; i < weight.size(); i++) { // 遍历物品
        for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量
            dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
        }
        for (int j = 0; j <= bagWeight; j++) {
            cout << dp[j] << " ";
        }
        cout << endl;
    }
    cout << dp[bagWeight] << endl;

}
int main() {
    test_multi_pack();
}

198. 打家劫舍 - 力扣（LeetCode）

你是一个专业的小偷，计划偷窃沿街的房屋。每间房内都藏有一定的现金，影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。

给定一个代表每个房屋存放金额的非负整数数组，计算你 不触动警报装置的情况下 ，一夜之内能够偷窃到的最高金额。

输入：[1,2,3,1]
输出：4
解释：偷窃 1 号房屋 (金额 = 1) ，然后偷窃 3 号房屋 (金额 = 3)。
     偷窃到的最高金额 = 1 + 3 = 4 。

确定dp数组（dp table）以及下标的含义：dp[i]：考虑下标i（包括i）以内的房屋，最多可以偷窃的金额为dp[i]。
确定递推公式：决定dp[i]的因素就是第i房间偷还是不偷。
- 如果偷第i房间，那么dp[i] = dp[i - 2] + nums[i] ，即：第i-1房一定是不考虑的，找出下标i-2（包括i-2）以内的房屋，最多可以偷窃的金额为dp[i-2] 加上第i房间偷到的钱。
- 如果不偷第i房间，那么dp[i] = dp[i - 1]，即考虑i-1房
dp数组如何初始化：从dp[i]的定义上来讲，dp[0] 一定是 nums[0]，dp[1]就是nums[0]和nums[1]的最大值即：dp[1] = max(nums[0], nums[1]);
dp[i] 是根据dp[i - 2] 和 dp[i - 1] 推导出来的，那么一定是从前到后遍历！
举例推导dp数组

class Solution {
public:
    int rob(vector<int>& nums) {
        if(nums.size() == 0)    return 0;
        if(nums.size() == 1)    return nums[0];
        vector <int> dp(nums.size(), 0);
        dp[0] = nums[0];
        dp[1] = max(nums[0], nums[1]);
        for(int i = 2; i < nums.size(); i++)
        {
            dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);
        }
        return dp[nums.size() - 1];
    }
};

213. 打家劫舍 II - 力扣（LeetCode）

你是一个专业的小偷，计划偷窃沿街的房屋，每间房内都藏有一定的现金。这个地方所有的房屋都 围成一圈 ，这意味着第一个房屋和最后一个房屋是紧挨着的。同时，相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警 。

给定一个代表每个房屋存放金额的非负整数数组，计算你 在不触动警报装置的情况下 ，今晚能够偷窃到的最高金额。

1
2
3

输入：nums = [2,3,2]
输出：3
解释：你不能先偷窃 1 号房屋（金额 = 2），然后偷窃 3 号房屋（金额 = 2）, 因为他们是相邻的。

和上一题差不多，就是首尾不能相连，变成环了。

考虑三种情况：

考虑不包含首尾元素
考虑包含首元素，不包含尾元素
考虑包含尾元素，不包含首元素

而情况二和情况三都包含了情况一了，所以只考虑情况二和情况三就可以了。

class Solution {
public:    
    int rob(vector<int>& nums) {
        if(nums.size() == 0)
        return 0;
        if(nums.size() == 1)
        return nums[0];
        int result1 = robRange(nums, 0, nums.size() - 2);
        int result2 = robRange(nums, 1, nums.size() - 1);
        return max(result1, result2);
    }
    int robRange(vector <int> nums, int start, int end)
    {
        if(end == start)
        return nums[start];
        vector <int> dp(nums.size());
        dp[start] = nums[start];
        dp[start + 1] = max(nums[start], nums[start + 1]);
        for(int i = start + 2; i <= end; i++)
        {
            dp[i] = max(dp[i - 1], dp[i - 2] + nums[i]);
        }
        return dp[end];
    }
};

337. 打家劫舍 III - 力扣（LeetCode）

小偷又发现了一个新的可行窃的地区。这个地区只有一个入口，我们称之为 root 。

除了 root 之外，每栋房子有且只有一个“父“房子与之相连。一番侦察之后，聪明的小偷意识到“这个地方的所有房屋的排列类似于一棵二叉树”。如果 两个直接相连的房子在同一天晚上被打劫 ，房屋将自动报警。

给定二叉树的 root 。返回 在不触动警报的情况下 ，小偷能够盗取的最高金额。

//时间复杂度：$O(n)$，每个节点只遍历了一次
//空间复杂度：$O(\log n)$，算上递推系统栈的空间
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int rob(TreeNode* root) {
        vector <int> result = robTree(root);
        return max(result[0], result[1]);
    }
    // 长度为2的数组，0：不偷，1：偷
    vector <int> robTree(TreeNode* cur){
        if(cur == NULL) 
        return vector <int> {0, 0};
        vector <int> left = robTree(cur->left);
        vector <int> right = robTree(cur->right);
        //偷cur
        int val1 = cur->val + left[0] + right[0];
        //不偷cur
        int val2 = max(left[0], left[1]) + max(right[0], right[1]);
        return {val2, val1};
    }
};

121. 买卖股票的最佳时机 - 力扣（LeetCode）

给定一个数组 prices ，它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。

你只能选择 某一天 买入这只股票，并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。

返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润，返回 0 。

输入：[7,1,5,3,6,4]
输出：5
解释：在第 2 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 6）的时候卖出，最大利润 = 6-1 = 5 。
     注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格；同时，你不能在买入前卖出股票。

动规五部曲：

dp[i][0] 表示第i天持有股票所得最多现金，dp[i][1] 表示第i天不持有股票所得最多现金。
确定递推公式：

如果第i天持有股票即dp[i][0]，那么可以由两个状态推出来
- 第i-1天就持有股票，那么就保持现状，所得现金就是昨天持有股票的所得现金即：dp[i - 1][0]
- 第i天买入股票，所得现金就是买入今天的股票后所得现金即：-prices[i]
- 那么dp[i][0]应该选所得现金最大的，所以dp[i][0] = max(dp[i - 1][0], -prices[i]);
如果第i天不持有股票即dp[i][1]，也可以由两个状态推出来
- 第i-1天就不持有股票，那么就保持现状，所得现金就是昨天不持有股票的所得现金即：dp[i - 1][1]
- 第i天卖出股票，所得现金就是按照今天股票佳价格卖出后所得现金即：prices[i] + dp[i - 1][0]
- 同样dp[i][1]取最大的，dp[i][1] = max(dp[i - 1][1], prices[i] + dp[i - 1][0]);

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int len = prices.size();
        if(len == 0)  return 0;
        vector <vector <int>> dp(len, vector <int> (2));
        dp[0][0] = -prices[0];
        dp[0][1] = 0;
        for(int i = 1; i < len; i++)
        {
            dp[i][0] = max(dp[i - 1][0], -prices[i]);
            dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + prices[i]);
        }
        return dp[len - 1][1];
    }
};

122. 买卖股票的最佳时机 II - 力扣（LeetCode）

给你一个整数数组 prices ，其中 prices[i] 表示某支股票第 i 天的价格。

在每一天，你可以决定是否购买和/或出售股票。你在任何时候最多只能持有一股股票。你也可以先购买，然后在 同一天 出售。

返回你能获得的最大利润。

输入：prices = [7,1,5,3,6,4]
输出：7
解释：在第 2 天（股票价格 = 1）的时候买入，在第 3 天（股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4 。
     随后，在第 4 天（股票价格 = 3）的时候买入，在第 5 天（股票价格 = 6）的时候卖出, 这笔交易所能获得利润 = 6 - 3 = 3 。
     总利润为 4 + 3 = 7 .

与上一题的唯一区别本题股票可以买卖多次了，dp数组和上一题的含义一致。

状态转移方程有些改变。上一题只能买入一次股票，因此dp[i][0] = max(dp[i - 1][0], -prices[i]);而本题可以买多次，因此dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i]);

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int len = prices.size();
        if(len == 0)  return 0;
        vector <vector <int>> dp(len, vector <int> (2));
        dp[0][0] = -prices[0];
        dp[0][1] = 0;
        for(int i = 1; i < len; i++)
        {
            dp[i][0] = max(dp[i - 1][0], dp[i - 1][1]-prices[i]);
            dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + prices[i]);
        }
        return dp[len - 1][1];
    }
};

123. 买卖股票的最佳时机 III - 力扣（LeetCode）

给定一个数组，它的第 i 个元素是一支给定的股票在第 i 天的价格。

设计一个算法来计算你所能获取的最大利润。你最多可以完成两笔交易。

注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

输入：prices = [3,3,5,0,0,3,1,4]
输出：6
解释：在第 4 天（股票价格 = 0）的时候买入，在第 6 天（股票价格 = 3）的时候卖出，这笔交易所能获得利润 = 3-0 = 3 。
     随后，在第 7 天（股票价格 = 1）的时候买入，在第 8 天 （股票价格 = 4）的时候卖出，这笔交易所能获得利润 = 4-1 = 3 。

与前两个题不同，关键在于至多买卖两次，这意味着可以买卖一次，可以买卖两次，也可以不买卖。

确定dp数组以及下标的含义一天一共就有五个状态。0：没有操作；1：第一次买入；2：第一次卖出；3：第二次买入；4：第二次卖出。dp[i][j]中 i表示第i天，j为 [0 - 4] 五个状态，dp[i][j]表示第i天状态j所剩最大现金。
确定递推公式：

dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] - price[i]

dp[i][2] = max(dp[i - 1][2], dp[i - 1][1] + price[i]

dp[i][3] = max(dp[i - 1][3], dp[i - 1][2] - price[i]

dp[i][4] = max(dp[i - 1][4], dp[i - 1][3] + price[i]
初始化：dp[0][0] = 0;dp[0][1] = -price[0];dp[0][2] = 0;dp[0][3] = -price[0];dp[0][4] = 0
遍历顺序为从前到后。
举例推导dp数组。

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int len = prices.size();
        vector<vector<int>> dp(len, vector<int>(5, 0));
        dp[0][1] = -prices[0];
        dp[0][3] = -prices[0];
        for(int i = 1; i < len; i++)
        {
            dp[i][0] = dp[i - 1][0];
            dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] - prices[i]);
            dp[i][2] = max(dp[i - 1][2], dp[i - 1][1] + prices[i]);
            dp[i][3] = max(dp[i - 1][3], dp[i - 1][2] - prices[i]);
            dp[i][4] = max(dp[i - 1][4], dp[i - 1][3] + prices[i]);
        }
    return dp[len - 1][4];
    }
};

188. 买卖股票的最佳时机 IV - 力扣（LeetCode）

给定一个整数数组 prices ，它的第 i 个元素 prices[i] 是一支给定的股票在第 i 天的价格。

设计一个算法来计算你所能获取的最大利润。你最多可以完成 k 笔交易。

注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

和上一题思路一样，就是把2换成了k。

class Solution {
public:
    int maxProfit(int k, vector<int>& prices) {
        int len = prices.size();
        if(!len) return 0;
        vector<vector<int>> dp(len, vector<int>(2 * k + 1, 0));
        for(int i = 1; i < 2 * k; i = i + 2)
        {
            dp[0][i] = -prices[0];
        }
        for(int i = 1; i < len; i++)
        {
            for(int j = 0; j < 2 * k - 1; j = j + 2)
            {
                dp[i][j + 1] = max(dp[i - 1][j + 1], dp[i - 1][j] - prices[i]);
                dp[i][j + 2] = max(dp[i - 1][j + 2], dp[i - 1][j + 1] + prices[i]);
            }
        }
    return dp[len - 1][2 * k];
    }
};

309. 最佳买卖股票时机含冷冻期 - 力扣（LeetCode）

给定一个整数数组prices，其中第 prices[i] 表示第 i 天的股票价格。

设计一个算法计算出最大利润。在满足以下约束条件下，你可以尽可能地完成更多的交易（多次买卖一支股票）:

卖出股票后，你无法在第二天买入股票 (即冷冻期为 1 天)。

注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

1
2
3

输入: prices = [1,2,3,0,2]
输出: 3 
解释: 对应的交易状态为: [买入, 卖出, 冷冻期, 买入, 卖出]

动规五部曲：

dp[i][j]，第i天状态为j，所剩的最多现金为dp[i][j]。

状态主要包括四种：
- 状态一：买入股票状态（今天买入股票，或者是之前就买入了股票然后没有操作）
- 状态二：两天前就卖出了股票，度过了冷冻期，一直没操作，今天保持卖出股票
- 状态三：今天卖出了股票
- 状态四：今天为冷冻期状态，但冷冻期状态不可持续，只有一天！

状态转移矩阵：

dp[i][0] = max(dp[i - 1][0], max(dp[i - 1][3], dp[i - 1][1]) - prices[i]);
dp[i][1] = max(dp[i - 1][1], dp[i - 1][3]);	//i - 1就是冷冻期或者i - 1已经度过了冷冻期
dp[i][2] = dp[i - 1][0] + prices[i];	//买入状态的最多现金 - 卖出赚的现金
dp[i][3] = dp[i - 1][2];	//卖出股票的下一天一定是冷冻期

初始化：dp[0][0] = -prices[0]，其余全为0.
遍历顺序：从前到后
模拟dp数组

//时间复杂度：$O(n)$
//空间复杂度：$O(n)$
class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int len = prices.size();
        if(len == 0) return 0;
        vector<vector<int>> dp(len,vector<int>(4,0));
        dp[0][0] = -prices[0];
        for(int i = 1; i < prices.size(); i++)
        {
            dp[i][0] = max(dp[i - 1][0], max(dp[i - 1][3], dp[i - 1][1]) - prices[i]);
            dp[i][1] = max(dp[i - 1][1], dp[i - 1][3]);
            dp[i][2] = dp[i - 1][0] + prices[i];
            dp[i][3] = dp[i - 1][2];
        }
        //返回状态二，状态三，和状态四的最大值
        return max(dp[len - 1][3],max(dp[len - 1][1], dp[len - 1][2]));
    }
};

714. 买卖股票的最佳时机含手续费 - 力扣（LeetCode）

给定一个整数数组 prices，其中 prices[i]表示第 i 天的股票价格；整数 fee 代表了交易股票的手续费用。

你可以无限次地完成交易，但是你每笔交易都需要付手续费。如果你已经购买了一个股票，在卖出它之前你就不能再继续购买股票了。

返回获得利润的最大值。

注意：这里的一笔交易指买入持有并卖出股票的整个过程，每笔交易你只需要为支付一次手续费。

输入：prices = [1, 3, 2, 8, 4, 9], fee = 2
输出：8
解释：能够达到的最大利润:  
在此处买入 prices[0] = 1
在此处卖出 prices[3] = 8
在此处买入 prices[4] = 4
在此处卖出 prices[5] = 9
总利润: ((8 - 1) - 2) + ((9 - 4) - 2) = 8

和122. 买卖股票的最佳时机 II - 力扣（LeetCode）相比添加了一个fee，只需要在dp数组的转移方程中将这部分减去即可。

class Solution {
public:
    int maxProfit(vector<int>& prices, int fee) {
        int len = prices.size();
        if(len == 0) return 0;
        vector<vector<int>> dp(len,vector<int>(2,0));
        dp[0][0] = -prices[0];
        for(int i = 1; i < prices.size(); i++)
        {
            //dp[i][0] 表示第i天持有股票所省最多现金
            dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i]);
            //dp[i][1] 表示第i天不持有股票所得最多现金
            dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + prices[i] - fee);
        }
        //返回状态二，状态三，和状态四的最大值
        return dp[len - 1][1];
    }
};