EasyRL-1
强化学习主要符号表:
| 主要符号表 | ||
|---|---|---|
| a:标量 | a:向量 | A:矩阵 |
| $\mathbb{R}$:实数集 | $arg_amaxf(a)$ :$f(a)$取最大值时a的值 | s:状态 |
| a:动作 | r:奖励 | $\pi$:策略 |
| $\gamma$:折扣因子 | $\pi(s)$:根据确定性策略$\pi$在状态$s$选取的动作 | $\tau$:轨迹 |
| $V_{\pi}(s)$:状态$s$在策略$\pi$下的价值 | $Q_{\pi}(s,a)$:状态$s$在策略$\pi$下采取动作$a$的价值 | $G_t$:时刻$t$的回报 |
| $\pi_{\theta}$:参数$\theta$对应的策略 | $J(\theta)$:策略$\pi_{\theta}$的性能度量 |
1.1 强化学习概述
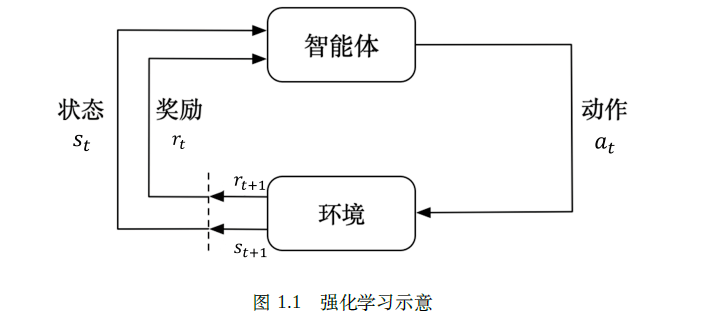
强化学习(reinforcement learning,RL)讨论的问题是智能体(agent)怎么在复杂、不确定的环境(environment)里面去最大化它能获得的奖励。
强化学习由两部分组成:智能体和环境。
在强化学习过程中,智能体与环境一直在交互。智能体在环境里面获取某个状态后,它会利用该状态输出一个动作(action),这个动作也称为决策(decision)。然后这个动作会在环境之中被执行,环境会根据智能体采取的动作,输出下一个状态以及当前这个动作带来的奖励。智能体的目的就是尽可能多地从环境中获取奖励。
监督学习的特点:输入的数据是没有关联的,且需要告诉学习器标签是什么。
强化学习这两点都不满足,以玩游戏为例,智能体得到的观测不是独立同分布的。(指随机过程中,任何时刻的取值都为随机变量,如果这些随机变量服从同一分布,并且互相独立,那么这些随机变量是独立同分布);上一帧与下一帧间其实有非常强的连续性;另外,我们并没有立刻获得反馈,游戏没有告诉我们哪个动作是正确动作,智能体不能立即得到反馈。
1.2 决策序列
环境有自己的函数${s_t}^e = f^e\left( H_t \right)$,智能体的内部也有一个函数${s_t}^a = f^a\left( H_t \right)$。
当智能体的状态与环境的状态等价的时候,即当智能体能够观察到环境的所有状态时,我们称这个环境是==完全可观测的==(fully observed)。在这种情况下面,强化学习通常被建模成一个马尔可夫决策过程(Markov decision process,MDP)的问题。在马尔可夫决策过程中,$o_t = {s_t}^e = {s_a}^e$
当智能体只能看到部分的观测,我们就称这个环境是==部分可观测的==(partially observed)。
在这种情况下,强化学习通常被建模成部分可观测马尔可夫决策过程(partially observable Markovdecision process, POMDP)的问题。部分可观测马尔可夫决策过程可以用一个七元组描述:$\left(S,A,T,R,\Omega,O,\gamma \right)$.中S 表示状态空间,为隐变量,A 为动作空间,
T(s′|s, a) 为状态转移概率,R 为奖励函数,Ω(o|s, a) 为观测概率,O 为观测空间,γ 为折扣因子。
1.3 动作空间
像雅达利游戏和围棋(Go)这样的环境有离散动作空间(discrete action space),在这个动作空间里,智能体的动作数量是有限的。
在其他环境,比如在物理世界中控制一个智能体,在这个环境中就有连续动作空间(continuous action space)。在连续动作空间中,动作是实值的向量。
1.4 智能体的组成成分和类型
对于一个强化学习智能体,它可能有一个或多个如下的组成成分。
策略(policy)。智能体会用策略来选取下一步的动作。
策略决定了智能体的动作,其包括随机性策略和确定性策略。
- 随机性策略(stochastic policy)就是$\pi$函数,即$\pi(a|s) = p(a_t = a | s_t = s)$。输入一个状态s,输出一个概率。
- 确定性策略就是智能体直接采取最有可能的动作,即$a^{*} = argmax \pi(a | s)$。
价值函数(value function)。我们用价值函数来对当前状态进行评估。价值函数用于评估智能体进入某个状态后,可以对后面的奖励带来多大的影响。价值函数值越大,说明智能体进入这个状态越有利。
我们可以把折扣因子放到价值函数的定义里面,价值函数的定义为:
$V_{\pi}(s) \doteq \mathbb{E}_{\pi}\left[G_{t} \mid s_{t}=s\right]=\mathbb{E}_{\pi}\left[\sum_{k=0}^{\infty} \gamma^{k} r_{t+k+1} \mid s_{t}=s\right]$
另外一种价值函数:Q函数
$Q_{\pi}(s, a) \doteq \mathbb{E}_{\pi}\left[G_{t} \mid s_{t}=s, a_{t}=a\right]=\mathbb{E}_{\pi}\left[\sum_{k=0}^{\infty} \gamma^{k} r_{t+k+1} \mid s_{t}=s, a_{t}=a\right]$
未来可以获得奖励的期望取决于当前的状态和当前的动作
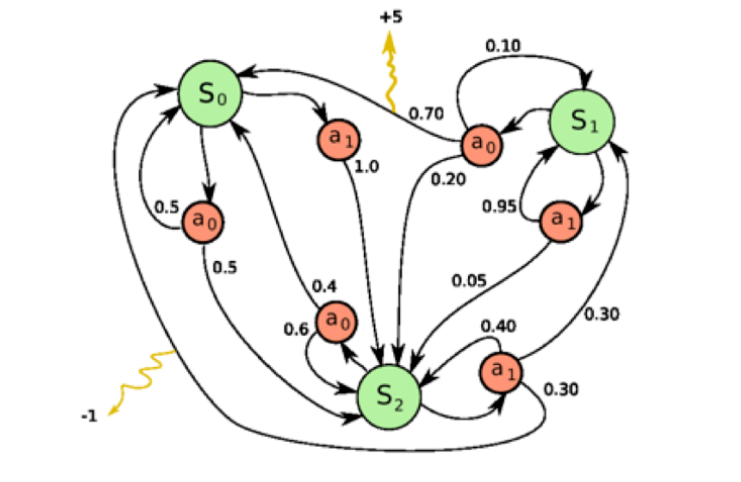
模型(model):模型表示智能体对环境的状态进行理解,它决定了环境中世界的运行方式。模型决定了下一步的状态。下一步的状态取决于当前的状态以及当前采取的
动作。它由状态转移概率和奖励函数两个部分组成。
状态转移概率: $p_{s s^{\prime}}^{a}=p\left(s_{t+1}=s^{\prime} \mid s_{t}=s, a_{t}=a\right)$
奖励函数: $R(s, a)=\mathbb{E}\left[r_{t+1} \mid s_{t}=s, a_{t}=a\right]$
当我们有了策略、价值函数和模型3 个组成部分后,就形成了一个马尔可夫决策过程(Markov decision process)
基于策略的强化学习(policy-based RL)方法:策略梯度算法等
当学习好了这个环境后,在每一个状态,我们都会得到一个最佳的动作。我们给它一个状态,它就会输出对应动作的概率。基于策略的智能体并没有学习价值函数。
基于价值的强化学习(value-based RL)方法:Q 学习(Q-learning)、Sarsa等
所以通过学习的价值的不同,我们可以抽取出现在最佳的策略。显式地学习价值函数,隐式地学习它的策略。策略是其从学到的价值函数里面推算出来的。这种方法只能应用在不连续的、离散的环境下(如围棋或某些游戏领域);对于动作集合规模庞大、动作连续的场景(如机器人控制领域),其很难学习到较好的结果(此时基于策略迭代的方法能够根据设定的策略来选择连续的动作)。
把基于价值的智能体和基于策略的智能体结合起来就有了演员-评论员智能体(actor-critic agent)。这一类智能体把策略和价值函数都学习了,然后通过两者的交互得到最佳的动作。其中,智能体会根据策略做出动作,而价值函数会对做出的动作给出价值,这样可以在原有的策略梯度算法的基础上加速学习过程,取得更好的效果。
有模型(model-based)强化学习智能体:
它通过学习状态的转移来采取动作。将任务表示成$
免模型(model-free)强化学习智能体:
它没有去直接估计状态的转移,也没有得到环境的具体转移变量。智能体只能在真实环境中通过一定的策略来执行动作,等待奖励和状态迁移,然后根据这些反馈信息来更新动作策略,这样反复迭代直到学习到最优策略。
利用OpenAI Gym 进行实验。是一个环境仿真库,里面包含了很多现有的环境
1 | # -*- coding: utf-8 -*- |
输出结果:
1 | 观测空间 = Box([-1.2 -0.07], [0.6 0.07], (2,), float32) |
总结一下 Gym 的用法:使用 env=gym.make(环境名) 取出环境,使用 env.reset()初始化环境,使用env.step(动作)执行一步环境,使用 env.render()显示环境,使用 env.close() 关闭环境。
