EasyRL-2
第2 章马尔可夫决策过程
智能体得到环境的状态后,它会采取动作,并把这个采取的动作返还给环境。环境得到智能体的动作后,它会进入下一个状态,把下一个状态传给智能体。在强化学习中,智能体与环境就是这样进行交互的,这个交互过程可以通过马尔可夫决策过程来表示,所以马尔可夫决策过程是强化学习的基本框架。
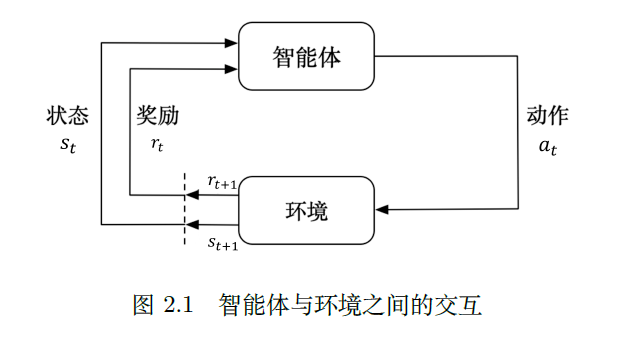
这部分介绍马尔可夫决策过程,先介绍它的简化版本:马尔可夫过程(Markov process,MP)以及马尔可夫奖励过程(Markov reward process,MRP)
其次,会介绍马尔可夫决策过程中的策略评估(policy evaluation),就是当给定决策后,我们怎么去计算它的价值函数。
最后,会介绍马尔可夫决策过程的控制,具体有策略迭代(policy iteration)和价值迭代(value iteration)两种算法。
2.1 马尔可夫过程
2.1.1 马尔可夫性质
马尔可夫性质(Markov property)是指一个随机过程在给定现在状态及所有过去状态情况下,其未来状态的条件概率分布仅依赖于当前状态。
$p\left(X_{t+1}=x_{t+1} \mid X_{0: t}=x_{0: t}\right)=p\left(X_{t+1}=x_{t+1} \mid X_{t}=x_{t}\right)$
其中,X0:t 表示变量集合X0,X1, · · · ,Xt,x0:t 为在状态空间中的状态序列x0, x1, · · · , xt。
马尔可夫性质也可以描述为给定当前状态时,将来的状态与过去状态是条件独立的。如果某一个过程满足马尔可夫性质,那么==未来的转移与过去的是独立的,它只取决于现在==。马尔可夫性质是所有马尔可夫过程的基础。
2.1.2 马尔可夫过程/马尔可夫链
马尔可夫过程是一组具有马尔可夫性质的随机变量序列$s_1,…,s_t$,其中下一个时刻的状态$s_{t+1}$ 只取决于当前状态$s_t$。我们设状态的历史为$h_t = \left\{s_1, s_2, … s_t\right\}$($h_t$ 包含了之前的所有状态),则马尔可夫过程满足条件:
$p\left(s_{t+1} \mid s_{t}\right)=p\left(s_{t+1} \mid h_{t}\right)$
从当前$s_t$ 转移到$s_{t+1}$ ,它是直接就等于它之前所有的状态转移到$s_{t+1}$ 。
离散时间的马尔可夫过程也称为马尔可夫链(Markov chain)
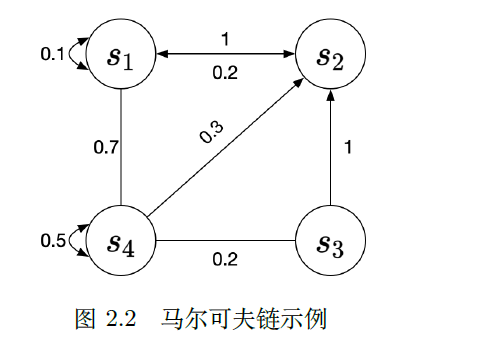
我们可以用状态转移矩阵(state transition matrix)P 来描述状态转移$p\left(s_{t+1}=s^{\prime} \mid s_{t}=s\right)$
$\boldsymbol{P}=\left(\begin{array}{cccc}p\left(s_{1} \mid s_{1}\right) & p\left(s_{2} \mid s_{1}\right) & \ldots & p\left(s_{N} \mid s_{1}\right) \ p\left(s_{1} \mid s_{2}\right) & p\left(s_{2} \mid s_{2}\right) & \ldots & p\left(s_{N} \mid s_{2}\right) \ \vdots & \vdots & \ddots & \vdots \ p\left(s_{1} \mid s_{N}\right) & p\left(s_{2} \mid s_{N}\right) & \ldots & p\left(s_{N} \mid s_{N}\right)\end{array}\right)$
状态转移矩阵类似于条件概率(conditional probability),它表示当我们知道当前我们在状态$s_t$ 时,到达下面所有状态的概率。所以它的每一行描述的是从一个节点到达所有其他节点的概率。
2.2 马尔可夫奖励过程
马尔可夫奖励过程(Markov reward process, MRP)是马尔可夫链加上奖励函数。奖励函数R 是一个期望,表示当我们到达某一个状态的时候,可以获得多大的奖励。这里另外定义了折扣因子γ。如果状态数是有限的,那么R 可以是一个向量。
2.2.1 回报与价值函数
$G_{t}=r_{t+1}+\gamma r_{t+2}+\gamma^{2} r_{t+3}+\gamma^{3} r_{t+4}+\ldots+\gamma^{T-t-1} r_{T}$
这里有一个折扣因子,越往后得到的奖励,折扣越多。当我们有了回报之后,就可以定义状态的价值了,就是状态价值函数(state-value function)。对于马尔可夫奖励过程,状态价值函数被定义成回报的期望,即:
$\begin{aligned} V^{t}(s) &=\mathbb{E}\left[G_{t} \mid s_{t}=s\right] \ &=\mathbb{E}\left[r_{t+1}+\gamma r_{t+2}+\gamma^{2} r_{t+3}+\ldots+\gamma^{T-t-1} r_{T} \mid s_{t}=s\right] \end{aligned}$
期望也可以看成未来可能获得奖励的当前价值的表现,就是当我们进入某一个状态后,我们现在有多大的价值。不同的折扣因子,可以得到不同的动作的智能体。
使用折扣因子的几个原因:
- 有些马尔可夫过程是带环的,避免无穷的奖励。
- 希望立即得到奖励,而不是未来得到奖励。
2.2.2 贝尔曼方程
从价值函数里面推导出贝尔曼方程
$V(s)=\underbrace{R(s)}_{\text {即时奖励 }}+\gamma \underbrace{\sum_{s^{\prime} \in S} p\left(s^{\prime} \mid s\right) V\left(s^{\prime}\right)}_{\text {末来奖励的折扣总和 }}$
贝尔曼方程定义了当前状态与未来状态之间的关系。未来奖励的折扣总和加上即时奖励,就组成了贝尔曼方程。
贝尔曼方程的推导过程如下:
$\begin{aligned} V(s) &=\mathbb{E}\left[G_{t} \mid s_{t}=s\right] \ &=\mathbb{E}\left[r_{t+1}+\gamma r_{t+2}+\gamma^{2} r_{t+3}+\ldots \mid s_{t}=s\right] \ &=\mathbb{E}\left[r_{t+1} \mid s_{t}=s\right]+\gamma \mathbb{E}\left[r_{t+2}+\gamma r_{t+3}+\gamma^{2} r_{t+4}+\ldots \mid s_{t}=s\right] \ &=R(s)+\gamma \mathbb{E}\left[G_{t+1} \mid s_{t}=s\right] \ &=R(s)+\gamma \mathbb{E}\left[V\left(s_{t+1}\right) \mid s_{t}=s\right] \ &=R(s)+\gamma \sum_{s^{\prime} \in S} p\left(s^{\prime} \mid s\right) V\left(s^{\prime}\right) \end{aligned}$
我们可以把贝尔曼方程写成矩阵的形式:
我们可以直接得到解析解(analytic solution):
$\boldsymbol{V}=(\boldsymbol{I}-\gamma \boldsymbol{P})^{-1} \boldsymbol{R}$
蒙特卡洛采样的方法:,从某一状态开始让其随机发展,当积累了一定数量的轨迹之后,我们直接用Gt 除以轨迹数量,就会得到某个状态的价值。
2.3 马尔可夫决策过程
相对于马尔可夫奖励过程,马尔可夫决策过程多了决策(决策是指动作),其他的定义与马尔可夫奖励过程的是类似的。马尔可夫决策过程满足条件:它也多了一个当前的动作 $p\left(s_{t+1} \mid s_{t}, a_{t}\right)=p\left(s_{t+1} \mid h_{t}, a_{t}\right)$
2.3.1 马尔可夫决策过程中的策略
策略定义了在某一个状态应该采取什么样的动作。知道当前状态后,我们可以把当前状态代入策略函数来得到一个概率,即 $\pi(a \mid s)=p\left(a_{t}=a \mid s_{t}=s\right)$
已知马尔可夫决策过程和策略π,我们可以把马尔可夫决策过程转换成马尔可夫奖励过程。 $P_{\pi}\left(s^{\prime} \mid s\right)=\sum_{a \in A} \pi(a \mid s) p\left(s^{\prime} \mid s, a\right)$
对于奖励函数,我们也可以把动作去掉,这样就会得到类似于马尔可夫奖励过程的奖励函数,即 $r_{\pi}(s)=\sum_{a \in A} \pi(a \mid s) R(s, a)$
2.3.2 马尔可夫决策过程和马尔可夫过程/马尔可夫奖励过程的区别
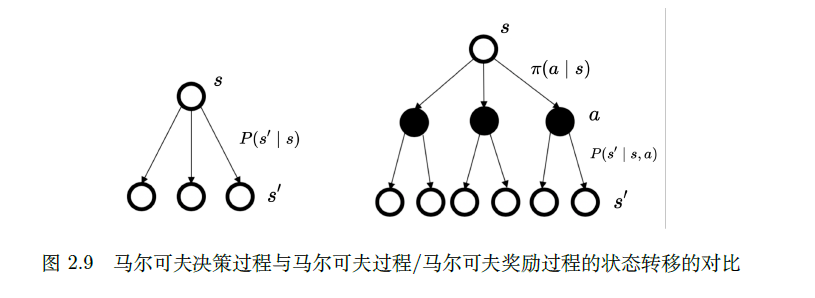
2.3.3 马尔可夫决策过程中的价值函数
马尔可夫决策过程中的价值函数可定义为: $V_{\pi}(s)=\mathbb{E}_{\pi}\left[G_{t} \mid s_{t}=s\right]$
其中,期望基于我们采取的策略。当策略决定后,我们通过对策略进行采样来得到一个期望,计算出它的价值函数。
这里我们另外引入了一个Q 函数(Q-function)。Q 函数也被称为动作价值函数(action-value function)。Q 函数定义的是在某一个状态采取某一个动作,它有可能得到的回报的一个期望,即 $Q_{\pi}(s, a)=\mathbb{E}_{\pi}\left[G_{t} \mid s_{t}=s, a_{t}=a\right]$
这里的期望其实也是基于策略函数的。所以我们需要对策略函数进行一个加和,然后得到它的价值。对Q函数中的动作进行加和,就可以得到价值函数: $V_{\pi}(s)=\sum_{a \in A} \pi(a \mid s) Q_{\pi}(s, a)$
2.3.4 贝尔曼期望方程
我们可以把状态价值函数和Q 函数拆解成两个部分:即时奖励和后续状态的折扣价值。通过对状态价值函数进行分解,我们就可以得到一个类似于之前马尔可夫奖励过程的贝尔曼方程——贝尔曼期望方程(Bellman expectation equation):
$V_{\pi}(s)=\mathbb{E}_{\pi}\left[r_{t+1}+\gamma V_{\pi}\left(s_{t+1}\right) \mid s_{t}=s\right]$
Q 函数的贝尔曼期望方程:
$Q_{\pi}(s, a)=\mathbb{E}_{\pi}\left[r_{t+1}+\gamma Q_{\pi}\left(s_{t+1}, a_{t+1}\right) \mid s_{t}=s, a_{t}=a\right]$
