2022-10-24

字数统计: 3.9k字 | 阅读时长: 17分

leetcode-hot-100-4

在一个由 '0' 和 '1' 组成的二维矩阵内，找到只包含 '1' 的最大正方形，并返回其面积。

动态规划的思想

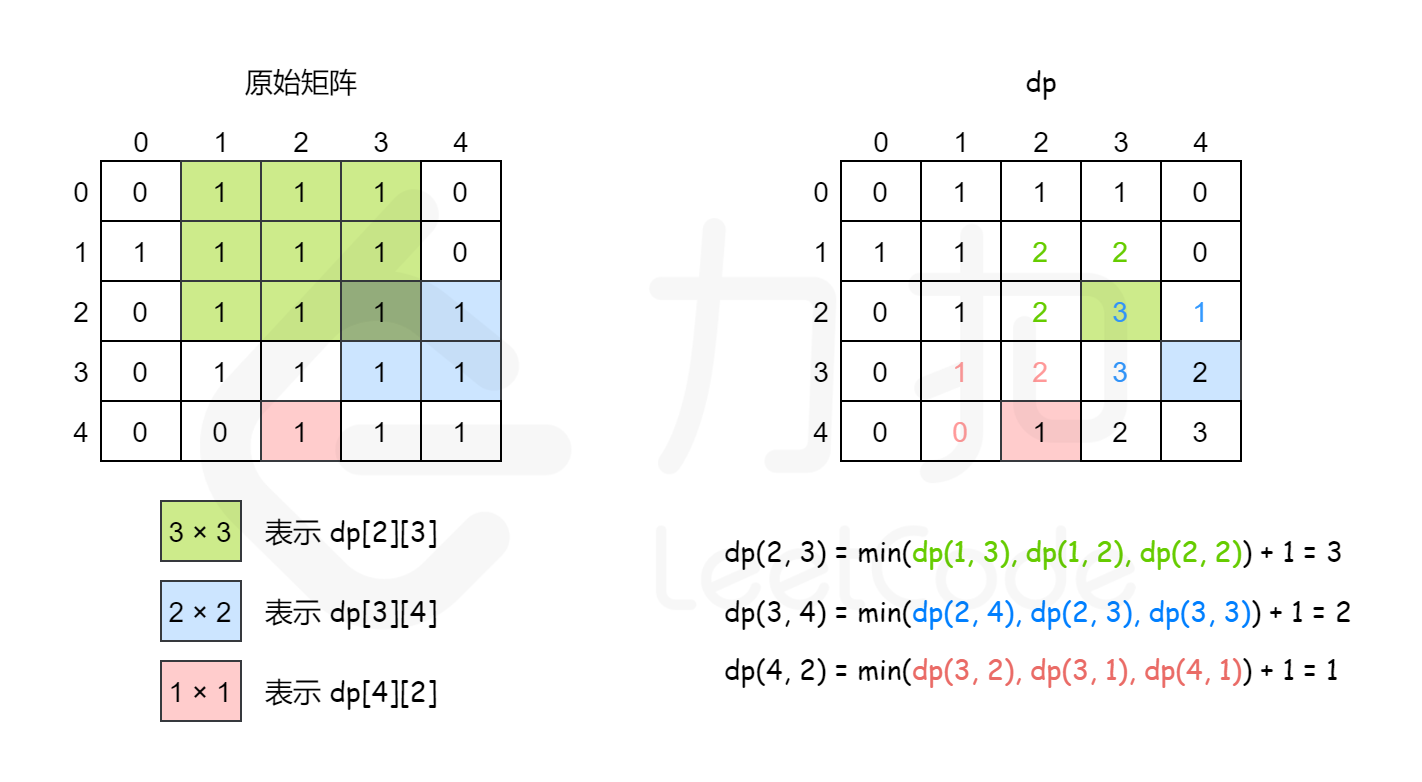
fig1

class Solution {
public:
    int maximalSquare(vector<vector<char>>& matrix) {
        int row = matrix.size();
        int col = matrix[0].size();
        int maxsize = 0;
        if(row == 0 || col == 0) {
            return 0;
        }
        vector <vector <int>> dp(row, vector<int> (col));
        for(int i = 0; i < row; i++) {
            for(int j = 0; j < col; j++) {
                if(matrix[i][j] == '1') {
                    if(i == 0 || j == 0) {
                        dp[i][j] = 1;
                    }
                    else {
                        dp[i][j] = min(min(dp[i - 1][j], dp[i][j - 1]), dp[i - 1][j - 1]) + 1;
                    }
                }
                maxsize = max(maxsize, dp[i][j]);
            }
        }
        return maxsize * maxsize;
    }
};

238. 除自身以外数组的乘积 - 力扣（LeetCode）

给你一个整数数组 nums，返回数组 answer ，其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积。

题目数据保证数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位整数范围内。

请不要使用除法，且在 O(n) 时间复杂度内完成此题。

基本思路如下：

原数组：       [1       2       3       4]
左部分的乘积：   1       1      1*2    1*2*3
右部分的乘积： 2*3*4    3*4      4      1
结果：        1*2*3*4  1*3*4   1*2*4  1*2*3*1

res先算 i 左边的所有数据的乘积，temp记录 i 右边所有数据的乘积，最后将两者乘起来

class Solution {
public:
    vector<int> productExceptSelf(vector<int>& nums) {
        vector<int> res(nums.size(), 1);
        vector<int> temp(nums.size(), 1);
        for (int i = 1; i < nums.size(); ++i) {
            res[i] = res[i - 1] * nums[i - 1];  //先算 i 左边所有元素的乘积
        }
        for (int i = nums.size() - 2; i >= 0; --i) {
            temp[i] = temp[i + 1] * nums[i + 1];    //temp[i]代表i右边所有元素的乘积
            res[i] = res[i] * temp[i];
        }
        return res;

    }
};

207. 课程表 - 力扣（LeetCode）

你这个学期必须选修 numCourses 门课程，记为 0 到 numCourses - 1 。

在选修某些课程之前需要一些先修课程。先修课程按数组 prerequisites 给出，其中 prerequisites[i] = [ai, bi] ，表示如果要学习课程 ai 则必须先学习课程 bi 。

例如，先修课程对 [0, 1] 表示：想要学习课程 0 ，你需要先完成课程 1 。
请你判断是否可能完成所有课程的学习？如果可以，返回 true ；否则，返回 false 。

用有向图描述依赖关系
示例：n = 6，先决条件表：[[3, 0], [3, 1], [4, 1], [4, 2], [5, 3], [5, 4]]
课 0, 1, 2 没有先修课，可以直接选。其余的课，都有两门先修课。
我们用有向图来展现这种依赖关系（做事情的先后关系）：

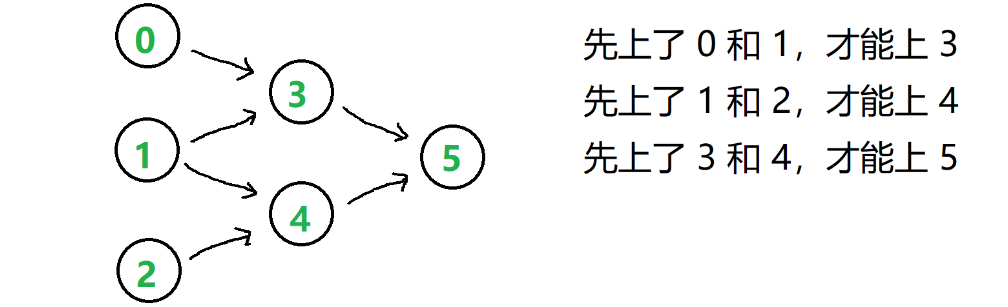
这种叫有向无环图，把一个有向无环图转成线性的排序就叫拓扑排序。
有向图有入度和出度的概念：
如果存在一条有向边 A —> B，则这条边给 A 增加了 1 个出度，给 B 增加了 1 个入度。
所以，顶点 0、1、2 的入度为 0。顶点 3、4、5 的入度为 2。

class Solution {
public:
    bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {
        vector<int> inDegree(numCourses);
        unordered_map<int, vector<int>> map;
        for (int i = 0; i < prerequisites.size(); i++) {
	        inDegree[prerequisites[i][0]]++;//当前课程入度值+1
	        map[prerequisites[i][1]].push_back(prerequisites[i][0]);//添加依赖他的后续课，key表示度为0的课，vector中存依赖key的后续课，也就是ai
        }
        queue<int> Qu;
        for (int i = 0; i < numCourses; i++) {
	        if (inDegree[i] == 0) Qu.push(i);//所有入度为0的课入列
        }
        int count = 0;
        while (Qu.size()) {
	        int selected = Qu.front();  //当前选的课
	        Qu.pop();//出列
	        count++;//选课数+1
	        vector<int> toEnQueue = map[selected];//获取这门课对应的后续课
	        if (toEnQueue.size()) { //确实有后续课
		        for (int i = 0; i < toEnQueue.size(); i++) {
			        inDegree[toEnQueue[i]]--; //依赖它的后续课的入度-1
			        if (inDegree[toEnQueue[i]] == 0) Qu.push(toEnQueue[i]); //如果因此减为0，入列
		        }
	        }
        }
        if (count == numCourses) return true;
        return false;
    }
};

240. 搜索二维矩阵 II - 力扣（LeetCode）

编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性：

每行的元素从左到右升序排列。
每列的元素从上到下升序排列。

考虑从右向左，从上向下遍历。这样如果当前元素大于target，向左走；当前元素小于target，向下走。

class Solution {
public:
    bool searchMatrix(vector<vector<int>>& matrix, int target) {
        int row = matrix.size();
        int col = matrix[0].size();
        int srow = 0;
        int scol = col - 1;
        while(srow < row && scol >= 0) {
            if(matrix[srow][scol] > target) {
                scol--;
            }
            else if(matrix[srow][scol] < target) {
                srow++;
            }
            else {
                return true;
            }
        }
        return false;
    }
};

Leetcode 253. 会议室 II C++解法_BlackJack1755的博客-CSDN博客

给你一个会议时间安排的数组 intervals ，每个会议时间都会包括开始和结束的时间 intervals[i] = [starti, endi] ，为避免会议冲突，同时要考虑充分利用会议室资源，请你计算至少需要多少间会议室，才能满足这些会议安排。

1 2	输入：intervals = [[0,30],[5,10],[15,20]] 输出：2

class Solution {
public:
    int minMeetingRooms(vector<vector<int>>& intervals) {
        if (intervals.size() == 0) {
            return 0;
        }

        vector<int> starts(intervals.size(), 0);
        vector<int> ends(intervals.size(), 0);
        for (int i = 0; i < intervals.size(); i++) {
            starts[i] = intervals[i][0];
            ends[i] = intervals[i][1];
        }
        sort(starts.begin(), starts.end());
        sort(ends.begin(), ends.end());

        auto startIter = starts.begin();
        auto endIter = ends.begin();
        int useRooms = 0 ;
        while (startIter != starts.end()) {
            if (*startIter >= *endIter) {
                useRooms -= 1;
                endIter++;
            }
            useRooms += 1;
            startIter++;
        }
        return useRooms;
    }
};

287. 寻找重复数 - 力扣（LeetCode）

给定一个包含 n + 1 个整数的数组 nums ，其数字都在 [1, n] 范围内（包括 1 和 n），可知至少存在一个重复的整数。

假设 nums 只有一个重复的整数，返回这个重复的数。

你设计的解决方案必须不修改数组 nums 且只用常量级 O(1) 的额外空间。

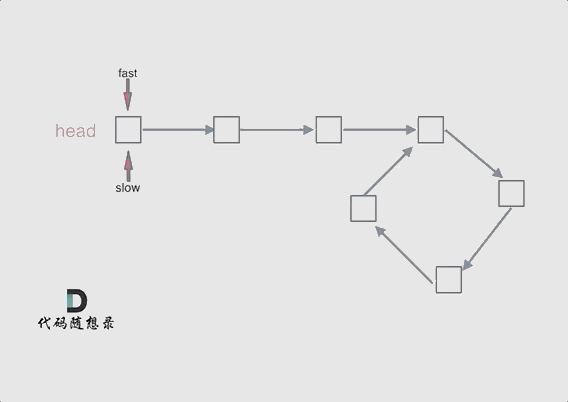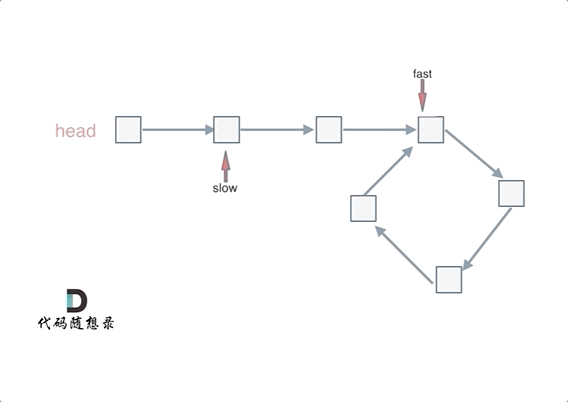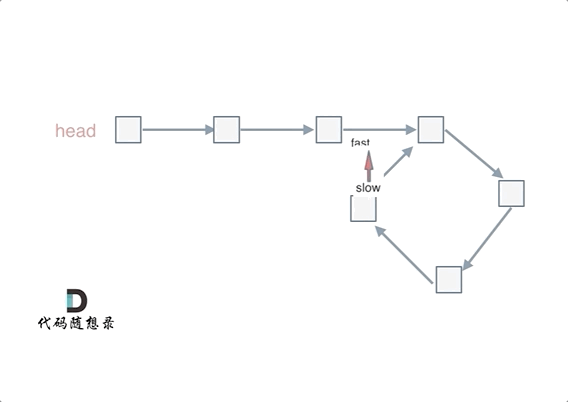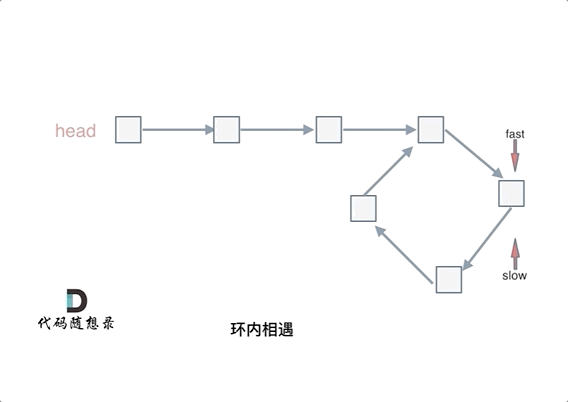
141.环形链表

//考虑环形链表的思路，如果有重复的数，一定成环，数组中如果有重复的数，那么就会产生多对一的映射，这样，形成的链表就一定会有环路了
class Solution {
public:
    int findDuplicate(vector<int>& nums) {
        int fast = 0, slow = 0;
        while(true){
            fast = nums[nums[fast]];
            slow = nums[slow];
            if(fast == slow)
                break;
        }
        int finder = 0;
        while(true){
            finder = nums[finder];
            slow = nums[slow];
            if(slow == finder)
                break;        
        }
        return slow;
    }
};

297. 二叉树的序列化与反序列化 - 力扣（LeetCode）

序列化是将一个数据结构或者对象转换为连续的比特位的操作，进而可以将转换后的数据存储在一个文件或者内存中，同时也可以通过网络传输到另一个计算机环境，采取相反方式重构得到原数据。

请设计一个算法来实现二叉树的序列化与反序列化。这里不限定你的序列 / 反序列化算法执行逻辑，你只需要保证一个二叉树可以被序列化为一个字符串并且将这个字符串反序列化为原始的树结构。

提示: 输入输出格式与 LeetCode 目前使用的方式一致，详情请参阅 LeetCode 序列化二叉树的格式。你并非必须采取这种方式，你也可以采用其他的方法解决这个问题。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */

class Codec {
public:

    // Encodes a tree to a single string.
    string serialize(TreeNode* root) {
        if(root==nullptr){
            return "#";
        }
        return to_string(root->val) + ' ' + serialize(root->left) + ' ' + serialize(root->right);   //把树转变为字符串
        //1 2 # # 3 4 # # 5 # #
    }

    TreeNode* mydeserialize(istringstream &ss ){
        string tmp;
        ss>>tmp;    //每次遇到空格前取出ss中的数据拿到tmp中
        if(tmp=="#"){
            return nullptr;
        }
        TreeNode* node = new TreeNode(stoi(tmp));
        node->left = mydeserialize(ss);
        node->right = mydeserialize(ss);
        return node;
    }

    // Decodes your encoded data to tree.
    TreeNode* deserialize(string data) {
        istringstream ss(data); //把data拷贝到istringstream ss中
        return mydeserialize(ss);
    }
};

// Your Codec object will be instantiated and called as such:
// Codec ser, deser;
// TreeNode* ans = deser.deserialize(ser.serialize(root));

301. 删除无效的括号 - 力扣（LeetCode）

给你一个由若干括号和字母组成的字符串 s ，删除最小数量的无效括号，使得输入的字符串有效。

返回所有可能的结果。答案可以按 任意顺序 返回。

思路：

首先我们令左括号的得分为 1；右括号的得分为 -1。则会有如下性质：

对于一个合法的方案而言，必然有最终得分为 0；
搜索过程中不会出现得分值为负数的情况（当且仅当子串中某个前缀中「右括号的数量」大于「左括号的数量」时，会出现负数，此时不是合法方案）。

枚举过程中出现字符分三种情况：

左括号：如果增加当前 ( 后，仍为合法子串（即 score + 1 <= max) 时，我们可以选择添加该左括号，也能选择不添加；
右括号：如果增加当前 ) 后，仍为合法子串（即 score - 1 >= 0) 时，我们可以选择添加该右括号，也能选择不添加；

普通字符：直接添加。

class Solution {
public:
    int maxscore;
    int length;
    int n;
    unordered_set<string> hash;

    void dfs(string s, int score, string buf, int l, int r, int index){
        if(l < 0 || r < 0 || score < 0 || score > maxscore) return;//如果出现删过头（即l或r<0）的情况，或分数出现负数或超过最大值，返回
        if(l == 0 && r == 0 && buf.length()==length) hash.insert(buf);
        if(index == n) return;

        char ch = s[index];
        if(ch=='('){
            dfs(s,score+1,buf+'(',l, r, index+1); //选择添加左括号，则+1分，继续遍历
            dfs(s,score,buf,l-1, r, index+1);//选择不添加左括号，相当于删除左括号，则分数不变，继续遍历
        }
        else if(ch==')'){
            dfs(s,score-1,buf+')',l, r, index+1);//选择添加右括号，则-1分，继续遍历
            dfs(s,score,buf,l, r-1, index+1);//选择不添加右括号，相当于删除右括号，则分数不变，继续遍历
        }
        else{
            dfs(s,score,buf+ch,l,r,index+1);//遇到其他字符，直接添加，继续遍历
        }
    }

    vector<string> removeInvalidParentheses(string s) {
        //假设“(”为+1分,")"为-1分，那么合规的字符串分数一定是0
        //分数一定不会是负数，因为那样意味着)比(多，不可能合规
        //分数一定不会超过maxscore，maxscore就是所有可匹配的(都在左边，一直+1，能达到的最大分数
        maxscore = 0;
        n = s.size();
        int left = 0;
        int right = 0;
        int l = 0,r = 0;
        length = 0;
        for(auto& ch : s){
            if(ch == '(') {//统计左括号数量
                l++; //需要删除的左括号数量
                left++;
            }
            else if(ch == ')'){//统计右括号数量
                if(l != 0) l--; //遇到可匹配的右括号
                else r++;//需要删除的右括号数量
                right++;
            }
        }
        length = n - l - r;//排除需要删除的左括号和右括号后，字符串应该有的长度
        maxscore = left < right? left : right;//最大分数为可匹配的左括号或右括号的数量，故为括号数量较少的那一边
        dfs(s, 0, "", l, r, 0);
        return {hash.begin(), hash.end()};
    }
};

312. 戳气球 - 力扣（LeetCode）

有 n 个气球，编号为0 到 n - 1，每个气球上都标有一个数字，这些数字存在数组 nums 中。

现在要求你戳破所有的气球。戳破第 i 个气球，你可以获得 nums[i - 1] nums[i] nums[i + 1] 枚硬币。这里的 i - 1 和 i + 1 代表和 i 相邻的两个气球的序号。如果 i - 1或 i + 1 超出了数组的边界，那么就当它是一个数字为 1 的气球。

输入：nums = [3,1,5,8]
输出：167
解释：
nums = [3,1,5,8] --> [3,5,8] --> [3,8] --> [8] --> []
coins =  3*1*5    +   3*5*8   +  1*3*8  + 1*8*1 = 167
戳破的顺序是1->5->3->8

[这个菜谱, 自己在家也能做] 关键思路解释 - 戳气球 - 力扣（LeetCode）

假设 dp[i][j] 表示开区间 (i,j) 内你能拿到的最多金币

假设 k 是最后一个被戳爆的，则

total=dp[i][k]+val[i] * val[k] * val[j] + dp[k][j]

class Solution {
public:
    int maxCoins(vector<int>& nums) {
        int n = nums.size();
        vector<vector<int>> dp(n + 2,vector<int>(n + 2,0));
        //创建一个辅助数组，并在首尾各添加1，方便处理边界情况
        vector<int> temp(n + 2);
        temp[0] = 1;
        temp[n + 1] = 1;
        for(int i = 1; i <= n; i++)
            temp[i] = nums[i - 1];
         //len表示开区间长度（对每一个区间长度进行循环）
        for(int len = 3; len <= n + 2; len++) {
            //l表示开区间左端点,l + len - 1则表示开区间右端点
            for(int l = 0; l <= n + 2 - len; l++) {
                //k为开区间内的索引（代表区间最后一个被戳破的气球）
                for(int k = l + 1; k < l + len - 1; k++) {
                    int left = dp[l][k];
                    int right = dp[k][l + len - 1];
                    int sum = left + right + temp[k] * temp[l] * temp[l + len - 1];
                    dp[l][l + len - 1] = max(dp[l][l + len - 1],sum);//取金币最大值
                }
            }
        }
        return dp[0][n + 1];
    }
};

399. 除法求值 - 力扣（LeetCode）

给你一个变量对数组 equations 和一个实数值数组 values 作为已知条件，其中 equations[i] = [Ai, Bi] 和 values[i] 共同表示等式 Ai / Bi = values[i] 。每个 Ai 或 Bi 是一个表示单个变量的字符串。

另有一些以数组 queries 表示的问题，其中 queries[j] = [Cj, Dj] 表示第 j 个问题，请你根据已知条件找出 Cj / Dj = ? 的结果作为答案。

返回所有问题的答案。如果存在某个无法确定的答案，则用 -1.0 替代这个答案。如果问题中出现了给定的已知条件中没有出现的字符串，也需要用 -1.0 替代这个答案。

注意：输入总是有效的。你可以假设除法运算中不会出现除数为 0 的情况，且不存在任何矛盾的结果。

输入：equations = [["a","b"],["b","c"]], values = [2.0,3.0], queries = [["a","c"],["b","a"],["a","e"],["a","a"],["x","x"]]
输出：[6.00000,0.50000,-1.00000,1.00000,-1.00000]
解释：
条件：a / b = 2.0, b / c = 3.0
问题：a / c = ?, b / a = ?, a / e = ?, a / a = ?, x / x = ?
结果：[6.0, 0.5, -1.0, 1.0, -1.0 ]

维护有向图，g[a][b]表示a / b；g[b][a]表示b / a

class Solution {
public:
    vector<double> calcEquation(vector<vector<string>>& equations, vector<double>& values, vector<vector<string>>& queries) {
        unordered_set<string> S;
        unordered_map<string, unordered_map<string, double>> g;
        for (int i = 0; i < equations.size(); i ++ )
        {
            auto a = equations[i][0], b = equations[i][1];
            auto c = values[i];
            g[a][b] = c;
            g[b][a] = 1.0 / c;
            S.insert(a);
            S.insert(b);
        }
        for (auto k: S)    // Floyd算法的核心：先枚举中间点，利用中间点来更新左右点的距离
        {
            for (auto i: S)
            {
                for (auto j: S)
                {
                    if (g[i][k] && g[j][k])
                        g[i][j] = g[i][k] * g[k][j];
                }
            }
        }
        vector<double> res;
        for (auto t: queries)
        {
            auto a = t[0], b = t[1];
            if (g[a][b])
                res.push_back(g[a][b]);
            else
                res.push_back(-1);
        }
        return res;
    }
};